
チャートは幾何学模様(?)
思考遊びとして。
ただ、ライントレーダーの自分としては、チャートを線ではなく‘面’で見ようとするのであればベースにしないといけないことだと勝手に思っている。
(「チャートは面で見ることが必要だ」と言っているわけではなくて、そういう方向を目指すならという意味)
・・・・・・・・・・・・・・・・・・・・・・
「チャートは幾何学模様だ。」という主張についてどう思うだろうか?
「そう見える人には見えるし、見えない人には見えない。」
まあ、これが答えだろう。
自分にとってはチャートは「幾何学模様以外の何物でもない」のだが、それは見た目の問題に加えて「リアルトレードの難しさ」ともリンクする。
特に`ペンローズタイル’、
これこそチャートが作られる手順と同じなのではないかと妄想すると、自分の中ではしっくり来る。
↓詳しくはこちらにて。(外部リンク)
https://www.google.com/amp/s/j344.exblog.jp/amp/17363319/
ペンローズタイルの作り方 | 幾何学模様のブログ みずすましの図工ノート
この幾何学模様は、「作り方の手順は周期的だけど、出来上がる模様は非周期的」という不思議なもの。
※「準周期的」というらしい。これを発案したペンローズ氏が、ノーベル賞を取ったことでまた知られることとなった。

この模様の「法則性」を見つけることができるだろうか? 法則と言えるくらい「多くの場合で当てはまり、それでいてシンプルな法則」があるだろうか。
初見では簡単に分かると思ってしまいそうだが、実は連なり方が複雑で分かりそうで分からない。パッと見て瞬時に逆算して作り方の手順が分かってしまう人もいるのだろうけど、そういう天才は除いてほとんどの人は法則が見つかりそうで見つからない。
それもそのはず、先述したように非周期的なのだから当たり前。
それでも何とか部分的にでも法則を見つけようと考えていると、「ヒトデ?星形?(もみじ饅頭?)そういう形が基本になっている。分けて考えるとひし形の連続になっているぞ。これが法則に違いない!」 と歓喜するも、緑や青は途中で破綻、紫にいたっては1つで終わり。

そして次に「いや、ひし形ばかりに気を取られていたけど、むしろその合間の💎っぽい形(黒枠)こそヒントだ。これが出たら隣にピンク&グレーのひし形が出るに違いない。」と発見するが、今度はこの形が出る機会が少なすぎる。

と、袋小路に迷い込んでいると、
「細かく見過ぎたらダメ。十角形(黒)で見るんだよ。」という声が聞こえてくる。
また、「解っていないな。五角形(赤)で考えるんだよ。」という声も聞こえる。
「いやいや、プロは対角線(青)を引くんだよ。」というも声も。
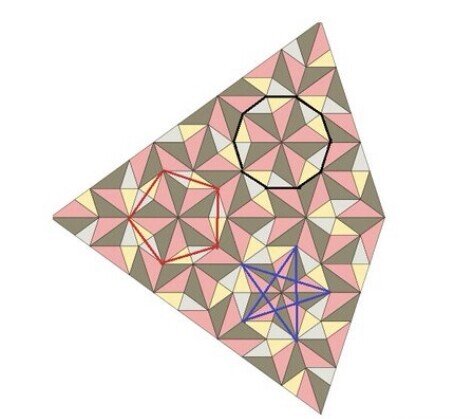
それらの声を参考に何とか法則を見つけようとして迷走し、
「ん?何の目的で試行錯誤してるんだっけ?」
と、タイルが並ぶ法則性を部分的にでも見つけるという目的を忘れて、外枠のことばかり考えていることに気づく。
と、ここまで読んで何が言いたいか分かった人もいると思うけど、これってチャートという幾何学模様を使ったトレードと同じではないかと。(いや、自分で考えた例えなんだが)
自分が持つべき視点のベクトルと、その焦点。
これをどこに置くのかを意識しながら考えることが大事で、そうでなければ当初の目的である「部分的にでも法則を見つける」ということからどんどんズレていってしまう。
本物のチャートでは、そもそもペンローズタイルでいう「タイルの形1つ1つの区切り」を認識すること自体が難しい。「ひし形」と思ったけど、後から見返すと微妙に変な形だったとか・・・。
そういう意味では、トレードというのはタイルの法則を当てるとかそういう単純なものではなく、真っ暗闇の中で谷底に落ちないように向こう側へジャンプしようとしているけど、果たして向こう側までの距離が自分のイメージと同じなのか分からない中、「いや、絶対3メートルのはず。」と何とか思い込んで飛び出す行為と似ている。飛べるかどうか以前に、距離の予想が合っているかも賭けになる。
と、幾何学模様の話からそれてしまったけれど、
「試行錯誤のベクトルが、自分の設定するゴールに向いているのか」
というのを意識しながら取り組むのが大事 だということ。
ちなみに、上記のペンローズタイルの法則だけど「頻出してシンプルな法則」があり、
それは、、、、
↓
↓
↓
「ピンクの長辺の隣は必ずグレー。その逆もしかり」という法則(?)がある。
長辺があるのはピンクとグレーしかなく、同じ色は隣には来ないのだから必然そうなるし、数も多いので最も目立つ法則と言って良いかと。最初にひし形で囲ったのはあえてのミスリードだけど、トレード界隈にもそういうことがたくさんある。。。
他人にとっての絶対法則は自分にとってはしばしば無益で、結局自分で試行錯誤して自分で見つけて、自分で実戦化するしかないっていう・・・。
ここから先は
この記事が気に入ったらチップで応援してみませんか?
