Cinderellaで数学:最大公約数と最小公倍数
2つの数の最大公約数と最小公倍数を作るプログラムをつくります。
最大公約数
まず、ある数の約数をすべてリストアップすることを考えます。CindyScriptのリスト処理をする関数を使うと次のように簡単にできます。
select(1 .. n, mod(n, #) == 0);1 .. n で、1からnまでの整数のリストを作成します。select関数は、そのリストから、mod(n, #) == 0 を満たすものを選び出してリストを作ります。mod(n, #) は、nを# ( #はリストの要素) で割った余りなので、mod(n, #) == 0 ということは「割り切れる」ということです。つまり,1からn までの数から,nを割りきる数,すなわち約数を選び出すのです。
たとえば、 n=12 のとき
1 .. n で、[1,2,3,4,5,6,7,8,9.10,11,12] というリストができます。その要素の始めから mod(12,#) つまり12をその要素で割った余りを調べて割り切れるものを選び出します。結果として 1,2,3,4,6,12 が選び出されます。
次に、これを関数にします。
divisor(n):= select(1 .. n, mod(n, #) == 0);これで、divisor(12) とすれば12の約数がリストアップされます。
結果をコンソールに表示しましょう。

2つの数に共通な約数が「公約数」です。そのうち最大のものが「最大公約数」です。では、2つの数の約数のリストを作り、最大公約数を求めてみましょう。2つの数の約数のリストは、それぞれ先ほどの処理で求められているとしましょう。CindyScriptには、2つのリストから共通な要素を抜き出すcommon(list1,list2)という関数があらかじめ用意されています。
divisor(n):= select(1 .. n, mod(n, #) == 0);
commondivisor(m,n) := common(divisor(m),divisor(n));とすれば,m とn の公約数のリストを作る関数ができます。

次に、最大公約数です。できた公約数のリストは昇順に並んでいるので,最後の要素を取り出せばいいのですが、CindyScriptには、リストの中から最大値をとり出す関数があり、中身がどんな順序になっていても構わないのでこれを使いましょう。

ユークリッドの互除法
2つの数の最大公約数を求める方法に、ユークリッドの互除法があります。
a, bの最大公約数を gcd(a, b) で表すことにします。いま、a>b とします。すると gcd(a, b) = gcd(a-b , b) が成り立ちます。
なぜなら、aとbの最大公約数をGとすると、
a=mG ・・ (1)
b=nG ・・ (2) m,nは互いに素
と表せるので a-b=(m-n)G です。このとき、m-nとnは互いに素なので(そうでないとすると、1でない公約数c があり m-n=ck , n=ch から m=ck+n=c(k+h) で mとnが互いに素でなくなります)(2)から、bとa-bの最大公約数はGということになります。つまり gcd(a,b)=gcd(a-b,b) です。
これをもう一度繰り返すと gcd(a,b)=gcd(a-b,b)=gcd(a-b-b,b) となります。つまり gcd(a,b)=gcd(a-2b,b) です。
さて、aをbで割った商をq , 余りを r とすると、a=bq+r となりますので
a-bq=r です。すると、 gcd(a,b)=gcd(a-b,b)=gcd(a-2b,b)=・・・=gcd(a-bq,b)=gcd(r,b) となり,結局
gcd(a,b)=gcd(b,r)
が成り立ちます。これがユークリッドの互除法の原理です。ややこしいですが,追えましたか。言葉でいうと、「aとbの最大公約数は、bと、aをbで割ったときの余り r との最大公約数に等しい」ということです。
すると、つぎに、「bとrの最大公約数は、rと、bをrで割ったときの余りr2との最大公約数に等しい」となり,「割った余り」が0でない限り、このことが繰り返されます。そして、最終的に「余りが0」になればそこで最大公約数が得られることになります。
具体的にやってみましょう。72と20でやります。
gcd(72,20) ・・・72を20で割ると余りは12
=gcd(20,12) ・・・20を12で割ると余りは8
=gcd(12,8) ・・・12を8で割ると余りは4
=gcd(8,4) ・・・8を4で割ると余りは0
ここで最後に割った数4が72と20の最大公約数です。
2つの数が互いに素の場合は次のようになります。
gcd(35,8) ・・・ 35を8で割ると余りは3
=gcd(8,3) ・・・ 8を3で割ると余りは2
=gcd(3,2) ・・・ 3を2で割ると余りは1
=gcd(2,1) ・・・ 2を1で割ると余りは0
最後に割ったのは1なので最大公約数は1,すなわち互いに素です。
では、これをCindyScriptで書いて見ましょう。「小さい方の数と、割った余りで考える」ということを何度も繰り返します。このような場合、「再帰的プログラム」という方法を使います。この「再帰的プログラム」は少し難しい概念ですので、何が何だか分からない、という人もいると思います。そのうちに慣れるでしょう。
aとbの最大公約数を求める関数をgcd(a, b) としましょう。この関数の処理の中で、aをbで割った余り r を求めて gcd(b, r) を求めます。すると、関数の処理の中で、自分自身の関数を使うことになります。これが「再帰的プログラム」です。
次のようになります。
gcd(a, b):=(
if(b == 0,
a;
,
if(b > a,
gcd(b, a);
,
gcd(b, mod(a, b));
);
);
);次が実行結果です。

最小公倍数
aとbの最大公約数を用いて最小公倍数を求めます。
aとbの最大公約数をGとすると
a=mG , b=nG (m,nは互いに素)
で、最小公倍数は mnG ですから、ab/G が最小公倍数となります。
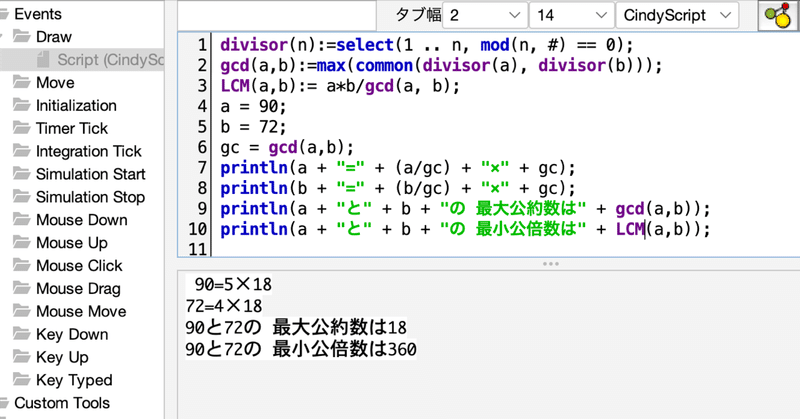
リストを使って最大公約数Gを求め、 ab/G で最小公倍数を表示しましょう。もちろん,ユークリッドの互除法で最大公約数を求めても結構です。リストを使う方がコードが簡単になります。
divisor(n):=select(1 .. n, mod(n, #) == 0);
gcd(a,b):=max(common(divisor(a), divisor(b)));
LCM(a,b):= a*b/gcd(a, b); 実行結果です。

見出し画像も参照してください。
