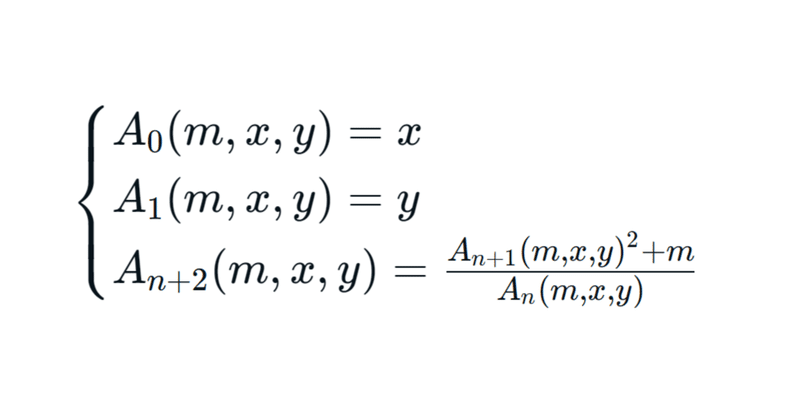
何だこの数列?
つい先日、こんな整数列に出会いました。
$${\begin{cases}a_0=a_1=1\\a_{n+2}=\frac{a_{n+1}^2+1}{a_n}\end{cases}}$$
ちょっと調べてみたところ面白い性質がいくつか見つかったので、この記事ではこの数列や関連する別の数列についてまとめます。
まずは計算してみる
まず、先程の漸化式を見て「これホントに整数列になるの?」と思った人が多いと思います。
とりあえず最初の数項を計算してみると、以下のようになります。
$${a_2=\frac{1^2+1}{1}=\frac{2}{1}=2}$$
$${a_3=\frac{2^2+1}{1}=\frac{5}{1}=5}$$
$${a_4=\frac{5^2+1}{2}=\frac{26}{2}=13}$$
$${a_5=\frac{13^2+1}{2}=\frac{170}{5}=34}$$
$${a_6=\frac{34^2+1}{13}=\frac{1157}{13}=89}$$
$${a_7=\frac{89^2+1}{34}=\frac{7922}{34}=233}$$
不思議なことに$${a_{n+1}^2+1}$$は毎回$${a_n}$$で割り切れ、整数列となっているように見えます。
ちなみに私がこの数列を発見した背景には、ソモスの数列という数列があります。
ソモスの数列というのは複数個の数列の総称なのですが、その中の「ソモスの第一数列」は以下の漸化式で定義されます。
$${\begin{cases}a_0=a_1=a_2=a_3=1\\a_{n+4}=\frac{a_{n+3}a_{n+1}+a_{n+2}^2}{a_n}\end{cases}}$$
この数列のように「定義式が分数式だけど必ず割り切れて整数列になる」という数列に興味が湧き、適当に漸化式を作って遊んでいたら見つかったのが冒頭の数列、というわけです。
話を戻します。
先程の2、5、13、34、89、233という値は、全てフィボナッチ数になっています。
フィボナッチ数列と照らし合わせてみると、以下のように$${a_n}$$は奇数番目のフィボナッチ数と一致しているように見えます。

ちなみにフィボナッチ数列の項番号を負の整数に(元の漸化式を満たすように)拡張すると$${F_{-1}=1}$$になるので、$${a_0=F_{-1}}$$と考えることができます。
ということは、$${a_0}$$を含むすべての項に対して$${a_n=F_{2n-1}}$$が成り立ちそうに見えます。
・・・なんで?
関連する数列群
$${a_n}$$の性質に深入りする前に、関連するほかの数列を紹介します。
$${\begin{cases}A_0(m,x,y)=x\\A_1(m,x,y)=y\\A_{n+2}(m,x,y)=\frac{A_{n+1}(m,x,y)^2+m}{A_n(m,x,y)}\end{cases}}$$
$${A_n(m,x,y)}$$は$${m,x,y}$$をそれぞれ固定することで定まる数列で、冒頭の数列は$${A_n(1,1,1)}$$に相当します。
$${x=y=1}$$として$${m}$$を動かすと、以下のような数列が生成されます。
$${A_n(2,1,1)=1,1,3,11,41,153,571…}$$
$${A_n(3,1,1)=1,1,4,19,91,436,2089…}$$
$${A_n(4,1,1)=1,1,5,29,169,985,5741…}$$
$${A_n(5,1,1)=1,1,6,41,281,1926,13201…}$$
$${A_n(0,1,1)=1,1,1,1,1,1,1…}$$
$${A_n(-1,1,1)=1,1,0,-1}$$※
$${A_n(-2,1,1)=1,1,-1,-1,1,1,-1…}$$
$${A_n(-3,1,1)=1,1,-2,1,1,-2,1…}$$
$${A_n(-4,1,1)=1,1,-3,5,-7,9,-11…}$$
$${A_n(-5,1,1)=1,1,-4,11,-29,76,-199…}$$
※0除算が発生するので第4項以降は無い
$${m=-1}$$以外は全て整数列になるようで、$${|m|}$$が十分大きいと$${A_n(1,1,1)}$$と同様に非自明な割り切りが生じるようです。
$${m=0}$$から$${m=-4}$$はあまり面白みは無く、それ以外はどれも見慣れない数列に思えるかもしれませんが、実は$${A_n(4,1,1)}$$は「ペル数列」という数列と関係しています。
ペル数列は、以下の漸化式で定義される数列です。
$${\begin{cases}P_0=0\\P_1=1\\P_{n+2}=2P_{n+1}+P_n\end{cases}}$$
$${P_n=0,1,2,5,12,29,70,169,408,985,2378,5741…}$$
ペル数列は「2-フィボナッチ数列」とも呼ばれ、一般に$${f_0(k)=0,f_1(k)=1,f_{n+2}(k)=kf_{n+1}(k)+f_n(k)}$$という形の数列を「$${k}$$-フィボナッチ数列」と呼ぶそうです。
$${A_n(1,1,1)}$$がフィボナッチ数列の奇数番目と一致するのと同様に、$${A_n(4,1,1)}$$はペル数列の奇数番目と一致しています。
もしやと思って計算してみると、$${A_n(9,1,1)}$$は3-フィボナッチ数列の奇数番目と一致し、一般に$${A_n(k^2,1,1)}$$は$${k}$$-フィボナッチ数列の奇数番目と一致するようです。
しかし、$${m}$$が平方数でないときの$${A_n(m,1,1)}$$については有名な数列の一部にはなっていないようでした。
項比の極限
フィボナッチ数列では$${\frac{F_{n+1}}{F_n}}$$の値が$${n→\infty}$$で$${\frac{1+\sqrt{5}}{2}}$$になるという性質が有名(多分)ですが、$${A_n(m,x,y)}$$でも同じような現象が見られました。
まず$${A_n(1,1,1)}$$では隣接する項の比は2.618ぐらいの定数に収束しますが、$${A_n(1,1,1)=F_{2n-1}}$$であることを考えるとこの値は$${(\frac{1+\sqrt{5}}{2})^2}$$であることがわかります。
同様に、$${A_n(k^2,1,1)}$$の項比の極限は$${k}$$-フィボナッチ数列の項比の2乗として求めることができ、その値は$${\frac{k^2+2+k\sqrt{k^2+4}}{2}}$$となります。
ここで$${k=\sqrt{m}}$$とすることで一般の$${A_n(m,1,1)}$$の項比を$${\frac{m+2+\sqrt{m^2+4m}}{2}}$$と推測することができ、実際に計算してみると$${m}$$が負でない場合は合っているようです。

※$${m=-1,-2,-3}$$のときは根号の中がマイナスになってしまい、$${m<-3}$$だと$${\frac{m+2-\sqrt{m^2+4m}}{2}}$$に収束するようになります。
フィボナッチ数列では初期値を変えても項比の極限は変わらないことが多いですが、$${A_n(m,x,y)}$$の項比の極限は$${x}$$と$${y}$$の値によって変わります。
例えば$${A_n(1,1,1)}$$の項比は先述の通り約2.618に収束しますが、初期値を変えただけの$${A_n(1,1,3)}$$の項比は3.370ぐらいの値に収束します。(ちなみに$${A_n(1,1,3)}$$は整数列にはなりません)
初期値を変えた際の項比をグラフにすると、以下のようになります。


どうやら$${\displaystyle{\lim_{n→\infty}\frac{A_{n+1}(1,x,y)}{A_n(1,x,y)}}}$$の値は$${x+\frac{1}{x}}$$のような「原点で発散し、原点から離れると直線に漸近する」という挙動を示し、漸近線の傾きは$${x}$$(gif動画では$${A_0}$$)の値によって変化するようです。
しかし、$${\displaystyle{\lim_{n→\infty}\frac{A_{n+1}(1,x,y)}{A_n(1,x,y)}}}$$の値を具体的に計算するのは難しそうです。
線形漸化式
$${A_n(m,x,y)}$$について色々と面白い性質が見えてきましたが、どれに関してもその仕組みは謎のままです。
何かヒントはないか、というか絶対何かしらの情報は載ってるだろうと考えてOEISで$${A_n(2,1,1)}$$の値を調べてみると、こんな情報がヒットしました。
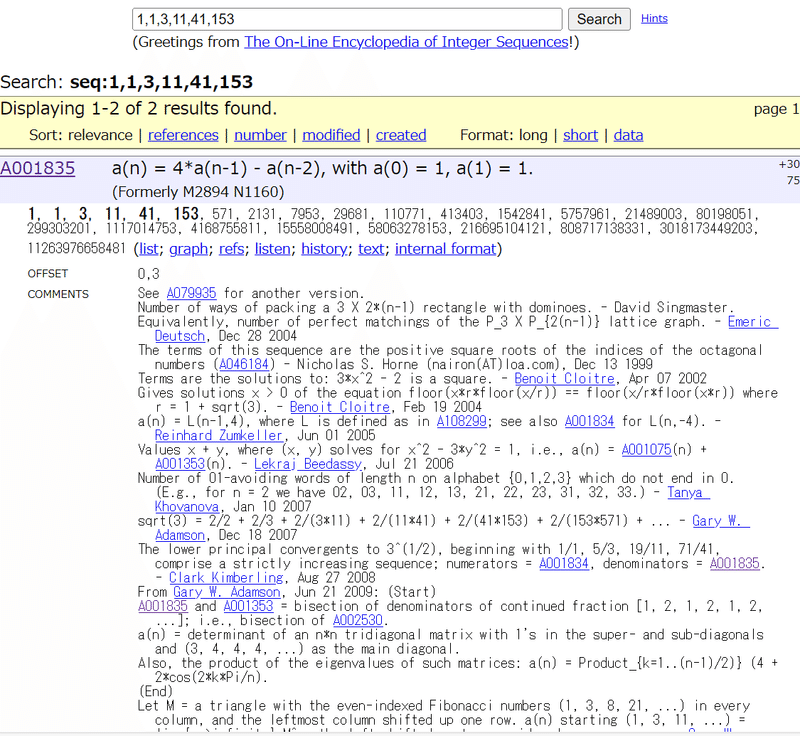
どうやら$${a_0=a_1=1,a_n=4a_{n-1}-a_{n-2}}$$という数列の値が$${A_n(2,1,1)}$$と一致するようです。(第6項以降の値も一致しています)
さらに$${A_n(1,1,1)}$$の値で検索すると、

$${a_0=a_1=1,a_n=3a_{n-1}-a_{n-2}}$$という数列がヒットします。($${A_n(3,1,1)}$$は検索しても何も出てきませんでした)
$${A_{n+2}(m,x,y)=\frac{A_{n+1}(m,x,y)^2+m}{A_n(m,x,y)}}$$という漸化式では扱いにくくて分析は困難ですが、線形漸化式(今回だと$${A_{n+1}(m,x,y)}$$と$${A_n(m,x,y)}$$についての1次式)で表せるなら状況は変わりそうです。
というわけで、まずは以下のようなことができないか考えました。
$${A_n(m,1,1)}$$が線形漸化式で表せると仮定し、$${A_{n+1}(m,1,1)}$$と$${A_n(m,1,1)}$$の係数を求める
1.で求めた漸化式が実際に正しいことを証明する
結論から言うと、この方法は成功します。(以下、$${A_n(m,1,1)}$$を$${A_n}$$と略記し、$${0< m}$$とします)
まず、$${A_{n+2}=aA_{n+1}+bA_n}$$が成り立つと仮定します。
この式を用いて$${A_2}$$と$${A_3}$$を計算し、定義通りに計算した値と比較すると以下の連立方程式が得られます。
$${\begin{cases}a+b=m+1\\a(m+1)+b=m^2+3m+1\end{cases}}$$
これを$${a,b}$$について解くと、$${a=m+2}$$、$${b=-1}$$になります。
次に、全ての非負整数$${n}$$について$${A_{n+2}=(m+2)A_{n+1}-A_n}$$が実際に成り立つことを証明します。
まず、先程の計算により$${n=0,1}$$のときに$${A_{n+2}=(m+2)A_{n+1}-A_n}$$が成り立つことがわかります。
次に、$${n=j}$$と$${n=j+1}$$のときに$${A_{n+2}=(m+2)A_{n+1}-A_n}$$が成り立つと仮定します。
このとき、$${A_{j+4}}$$は以下のように変形できます。
$${A_{j+4}\\=\frac{A_{j+3}^2+m}{A_{j+2}}\\=\frac{A_{j+3}((m+2)A_{j+2}-A_{j+1})+m}{A_{j+2}}\\=\frac{(m+2)A_{j+3}A_{j+2}-A_{j+3}A_{j+1}+m}{A_{j+2}}\\=(m+2)A_{j+3}-\frac{A_{j+3}A_{j+1}-m}{A_{j+2}}\\=(m+2)A_{j+3}-\frac{1}{A_{j+2}}(\frac{A_{j+2}^2+m}{A_{j+1}}×A_{j+1}-m)\\=(m+2)A_{j+3}-A_{j+2}\\}$$
よって、$${n=j}$$と$${n=j+1}$$のとき$${A_{n+2}=(m+2)A_{n+1}-A_n}$$が成り立てば$${n=j+2}$$のときも成り立ちます。
以上より、数学的帰納法により全ての非負整数$${n}$$について$${A_{n+2}=(m+2)A_{n+1}-A_{n}}$$が成り立つことがわかります。
$${A_n(m,1,1)}$$が整数係数の線形漸化式で表せることが分かったので、$${m}$$が正の整数のときに$${A_n(m,1,1)}$$が整数になることがわかります。(「なぜ割り切れるのか」という感覚的疑問は解消されませんが)
ちなみに$${m}$$が負の場合、上記の証明に加えて$${A_{j+2}}$$と$${A_{j+1}}$$が0でないことを示す必要があります。
実際、$${A_2=0}$$となり$${A_3}$$までしか計算できない$${m=-1}$$のケースでは、線形漸化式で計算することにより存在しないはずの第4項以降が計算できてしまいます。
$${A_n(k^2,1,1)}$$が$${k}$$-フィボナッチ数列の奇数番目になるという性質も、$${A_n(m,1,1)}$$が線形漸化式で表せるという性質で説明できます。
$${A_n(k^2,1,1)=f_{2n-1}(k)}$$が成り立つという事は、$${A_n(k^2,1,1)}$$と$${f_{2n-1}(k)}$$は同じ初期値を持ち、同じ形の漸化式に従わなければなりません。
つまり、以下の3つの条件が成り立たなければなりません。
$${f_{-1}(k)=1}$$
$${f_1(k)=1}$$
$${f_{2n+3}(k)=(k^2+2)f_{2n+1}(k)-f_{2n-1}(k)}$$
2番目の条件は定義から明らかで、1番も簡単に確かめられるので、3番目が成り立つことを確認します。
まず、$${k}$$-フィボナッチ数列の定義式の$${f_{n+2}(k)=kf_{n+1}(k)+f_n(k)}$$を変形することで$${kf_{n}(k)=f_{n+1}(k)-f_{n-1}(k)}$$という式が得られます。
この式を利用すると、$${f_{2n+3}(k)}$$は以下のように変形できます。
$${f_{2n+3}(k)=kf_{2n+2}(k)+f_{2n+1}(k)\\=k(kf_{2n+1}(k)+f_{2n}(k))+f_{2n+1}(k)\\=(k^2+1)f_{2n+1}(k)+kf_{2n}(k)\\=(k^2+1)f_{2n+1}(k)+f_{2n+1}(k)-f_{2n-1}(k)\\=(k^2+2)f_{2n+1}(k)-f_{2n-1}(k)}$$
よって、$${A_n(k^2,1,1)=f_{2n-1}(k)}$$が成り立ちます。
ちなみに、同じ考え方により$${m}$$が平方数でないときの$${A_n(m,1,1)}$$を「線形三項間漸化式で表せる数列の奇数番目」として表すこともできますが、その場合の$${f_n}$$に相当する数列は整数列にはならないようでした。
最後に、$${\displaystyle{\lim_{n→\infty}\frac{A_{n+1}(m,x,y)}{A_n(m,x,y)}}}$$の値を求めるのにも線形漸化式が使えます。
$${A_n(m,1,1)}$$とほとんど同じ手順により$${A_n(m,x,y)}$$も線形三項間漸化式で表すことができ、具体的には
$${A_{n+2}(m,x,y)=\frac{x^2+y^2+m}{xy}A_{n+1}(m,x,y)-A_n(m,x,y)}$$
・・・という式が求まります。
線形漸化式にさえなってしまえば、特性方程式から項比を求めることができ、実際に計算すると以下のようになります。
$${\displaystyle{\lim_{n→\infty}\frac{A_{n+1}(m,x,y)}{A_n(m,x,y)}}=\frac{x^2+y^2+m+\sqrt{(x^2+y^2+m)^2-4x^2+y^2}}{2xy}}$$
おまけ
おまけです。
似たような数列
$${A_n(m,1,1)}$$のような「何故か整数になる数列」を他に2つ発見しました。
$${\begin{cases}b_0=b_1=1\\b_{n+2}=\frac{b_{n+1}^3+1}{b_n}\end{cases}}$$
$${b_n=1,1,2,9,365,5403014,432130991537958813…}$$
$${\begin{cases}c_0=c_1=c_2=1\\c_{n+3}=\frac{c_{n+2}c_{n+1}+1}{c_n}\end{cases}}$$
$${c_n=1,1,1,2,3,7,11,26,41,97…}$$
残念ながらどちらの数列もOEISに載っていました。
謎の等式
wikipediaのフィボナッチ数のページにはこんな式が載っています。
$${F_{n-1}F_{n+1}-F_n^2=(-1)^n}$$
$${n}$$を$${2n}$$に置き換えて変形すると$${F_{2n+1}=\frac{F_{2n}^2+1}{F_{2n-1}}}$$という式になり、$${A_n(1,1,1)}$$の定義式と似た形になります。
なので$${A_n(1,1,1)=F_{2n-1}}$$の証明に使えると思ったのですが、実際は上手くいきませんでした。
バグったgif

サイズの大きいgif動画をnoteに貼り付けるとこんな感じにバグることがあります。
追記
続きです。
