『物性物理学１』§１：自由電子モデルの効用と限界

（１）古典論（粒子）にもとづくモデル（電気伝導）

1896(1897?)年にJ. J. Thomsonによって電子が発見された数年後の1900年に、Paul Drudeによって、「電子がどう流れるのか？」についてDrude理論が提案された。

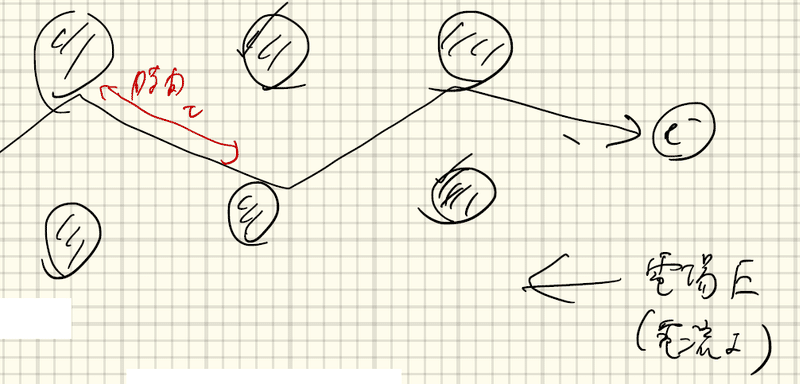
金属を考えて、電場E（電流I）をかける。前述の通り、物質中では原子核が周期的に並んでおり、自由電子が（電場と反対方向に）格子と衝突しながら進む。

格子との衝突の平均の時間間隔をτとおく。時刻t+dtにおける運動量pについて、

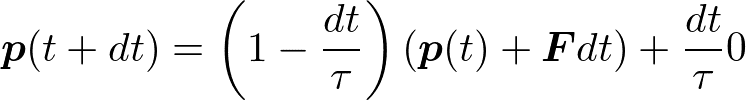
と書ける。dt/τが散乱する確率を表しており、第一項は散乱されないときに運動量はどう増えるか（ここでFは力である）が書いてある。第二項は散乱されたときに運動量がゼロになることを意味する。上式を変形すると、

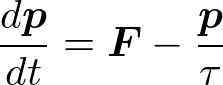
電場がかかった状態では、

である。定常状態では、dp/dt=0であり、

が得られる。電流は、

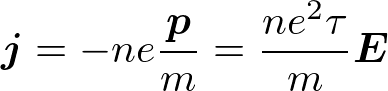
と書ける。これがオームの法則であり、電気伝導度は

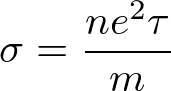
と表せる。直感的にはわかりやすいが、定量的にはあまり合わないことが知られる。

（２）量子論（波動）に基づくモデル

金属では、電子は原子核からの束縛を離れて、伝導電子として結晶中を動き回る。これを§０では電子の波動性と関連付けて説明した。

ここでは電子を波（波動関数）としてとらえ、量子力学的に考察する。

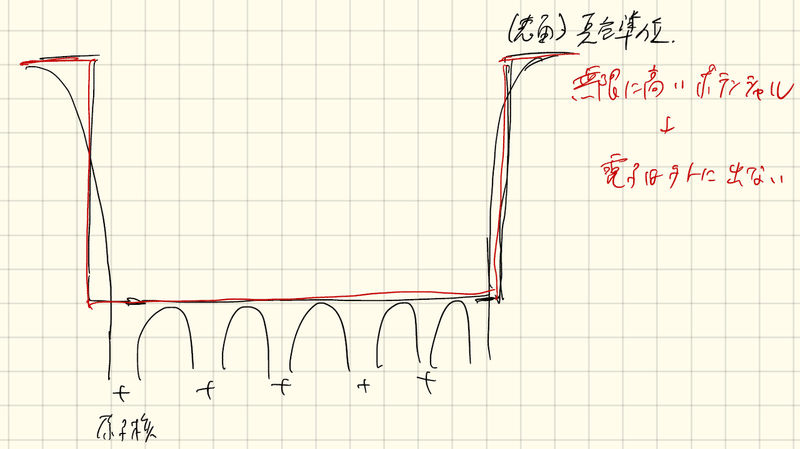
物質の表面には無限に高いポテンシャルがあると考え、電子は外に出ないとする。物質中は＋電荷の原子核が周期的に並んでいる（周期ポテンシャルがある）が、周期ポテンシャルをならして平坦とする。つまり、井戸型ポテンシャルを考える。また、金属中の電子は”自由電子”とする。

時間に依存しないシュレディンガー方程式

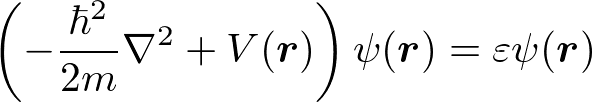
を考える。ポテンシャルVは、V=L^3の箱を考え、

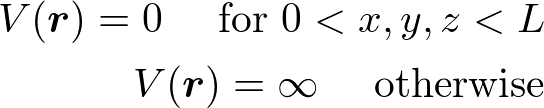
とおく。平面波解

を仮定して代入すると、エネルギーについて

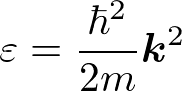
である。この波動関数は、電子がいたるところに広がっている状態を表している。

ここで、波動関数について周期境界条件を課す。

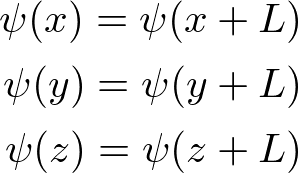
周期境界条件は、計算が簡単になる境界条件であり、端が関係しないほとんどの物性は境界条件に依存しないことが知られている（結晶は通常大きいので表面の効果は見えず、物性は境界条件のとり方によらない結果となるため、計算の簡単になる境界条件をとろうということ）。境界条件に波動関数の平面波解を代入すると、

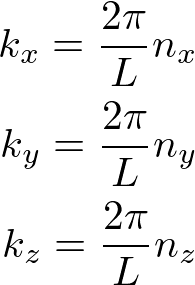
となる。ここで、n_x, n_y, n_zは整数である。このように電子は波であるが、波数ｋは離散的である。

電子はフェルミ粒子であり、以下の分布関数に従う。

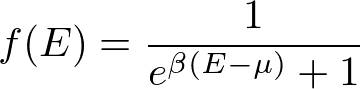
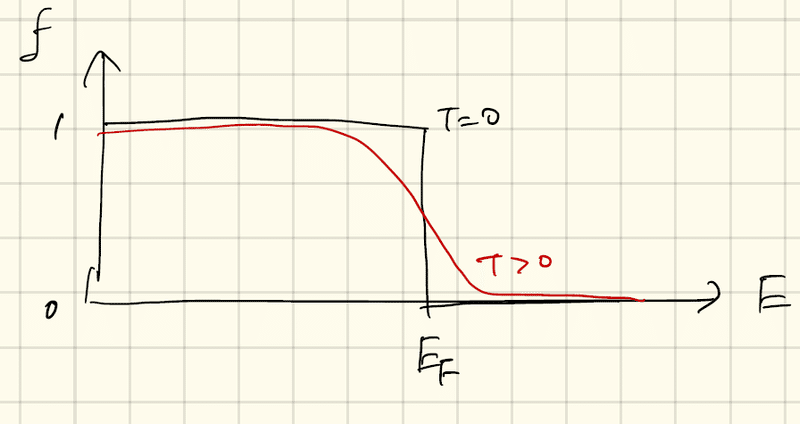
フェルミの分布関数は0から１の値をとり、一つのエネルギー準位にある粒子の数（占有数）の分布を与える。１つより多くの電子が入らないのは、パウリの原理のためである。E_FはT=0での化学ポテンシャルであり、フェルミエネルギーと呼ばれる。温度が0Kから上がると、E_Fより高いエネルギーをもつことができる。

フェルミエネルギーの大きさは、E_F ~ 10^5 K  (>>室温）と非常に大きい。（これは後で導出する。）電気伝導はフェルミエネルギー付近の電子のみが寄与するので、エネルギーの高い電子が流れている。

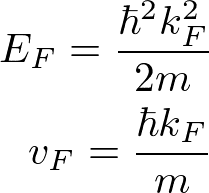
古典論モデルと量子論モデルでの主な違いはこの部分にある。つまり、古典論モデルにおいては、電子の運動エネルギーは熱エネルギーであり、

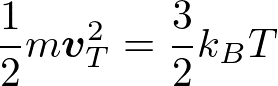
である。温度は室温で300 Kである。一方、前述の通り、量子論モデルにおいてはフェルミエネルギーのスケールであり、

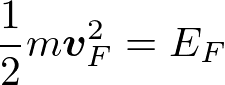
と書ける。電子のもつ速さの比は、

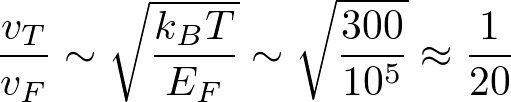
くらいである。要するに、古典論では電子の速さを過小評価していることになる。（なお、電子の比熱も古典論では合わないことが知られている。）

しかしながら、定性的にはDrudeモデルは悪くない。その理由としては

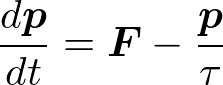
というDrudeの式は、フェルミ面付近の電子達の重心（つまり平均）に対しても使えるからである。１つの電子はv_Fという速い速度をもつが、多くの電子が色んな方向に走っていれば平均の速度はゼロである。電場がかかれば平均として速度ゼロだった電子達が電場で加速され、そして格子との散乱によってエネルギーを失い、フェルミエネルギーの下の準位に落ちる。この過程はDrudeモデルで考えたことと同じである。

＊フェルミエネルギーの計算

先ほどとばしたフェルミエネルギーの計算をここで確認する。

電子の数は、

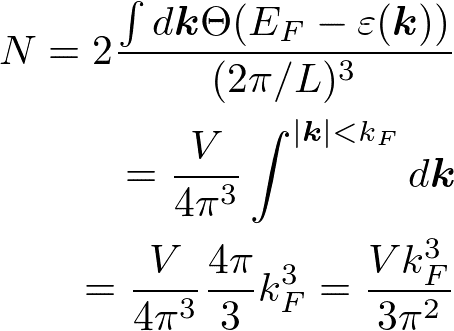
と書ける。最初の２はスピン自由度であり、T=0でE_F以下にある状態の数を考えている。T＝０でE_F以下のエネルギー準位は詰まっているので、電子の数に等しい。電子密度は、n=N/Vであり、

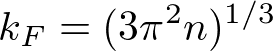
より、

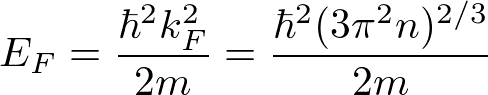
となる。n= 1 x 10^23 cm^-3 を仮定すると、E_F ~ 8 eVになる。これはk_Bで割ると、90000 Kに相当する。

（３）自由電子モデルの欠点（いくつか）

①散乱の平均自由行程は、~1 mmに及ぶことがある。一方、格子間隔（原子核同士の間隔）は~ Åレベルである。なぜ散乱されないのか。

②原子の内殻電子は、E_Fを計算するときには関係ない。これは何故か。

③いっぱい電子がいるのに、電子同士の相互作用はなぜ無視できるのか。

これらの問の答えは、今後の学習によって理解される。

この節の内容は、

『The Oxford Solid State Basics』（Steven H. Simon）

『電気伝導入門』（前田京剛）

に詳しい。