第４回 トーラス盤上の駒

前回の続きです。

---

無限盤上の駒（の利き）は$${\mathbb{Z}\times\mathbb{Z} }$$の部分集合のことであると定義しました。

同様に、$${9\times 9}$$のトーラス盤上の駒（の利き）は$${\mathbb{Z}/9\mathbb{Z}\times\mathbb{Z}/9\mathbb{Z} }$$の部分集合のことと定義します。

なお、$${\mathbb{Z}/9\mathbb{Z}}$$は整数を$${9}$$で割ったときの余りで整数をグルーピングした集合です。

$${9}$$で割った余りが例えば$${4}$$である整数の集合を

$$
\overline{4}=\{ \cdots ,-14,-5, 4,13,21,\cdots \}
$$

のように表します。

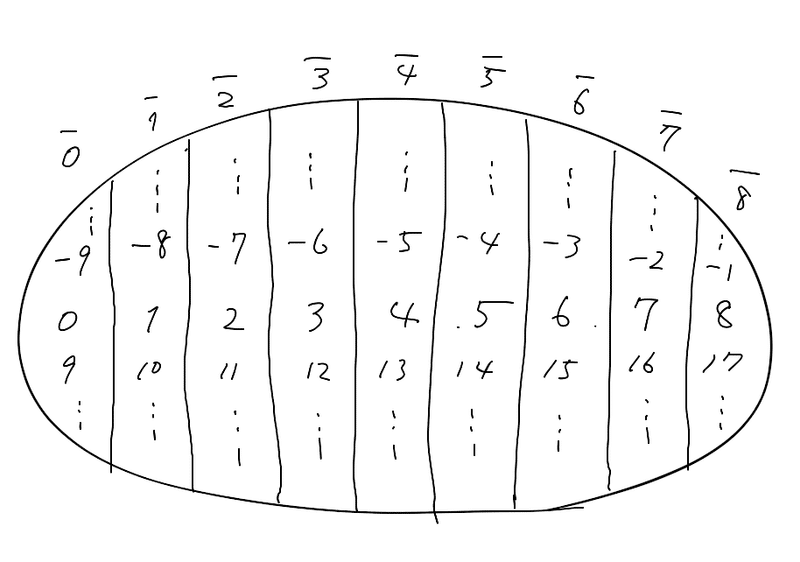
同じグループの整数ならば、$${\overline{4}=\overline{13}}$$のような等式が成り立ちます。余りで分けたグループの集合が$${\mathbb{Z}/9\mathbb{Z}}$$です。

$$
\mathbb{Z}/9\mathbb{Z}=\{\overline{0},\overline{1},\overline{2},\overline{3},\overline{4},\overline{5},\overline{6},\overline{7},\overline{8}\}
$$

$${\mathbb{Z}/9\mathbb{Z}}$$では足し算・引き算・掛け算が定義でき、例えば足し算は、

$$
\overline{a}+\overline{b} = \overline{a+b}
$$

で定義されます。

また、毎回毎回「$${\bar{}}$$」を書いていると煩雑になるので、

$$
\mathbb{Z}/9\mathbb{Z}=\{0,1,2,3,4,5,6,7,8\}
$$

と略記します。

結局のところ$${\mathbb{Z}/9\mathbb{Z}}$$とは、$${9}$$で割った余りが等しい整数は等しいと見なす世界です。

$${\mathbb{Z}/9\mathbb{Z}}$$上では例えば

$$
\begin{align*}
&4+8=12=3, \\
&2-7=-5=4, \\
&4\cdot 6=24=6, \\
&3\cdot 3=9=0
\end{align*}
$$

のように計算ができます。$${9=0}$$なので、$${9}$$をいくら足し引きしても等号が成り立ちます。

では、トーラス盤上で桂馬の利きを見てみましょう。

例４.１
桂馬の利きは

$$
\text{桂}=\{(1,2),(-1,2)\}
$$

だが、トーラス盤上で考えると（$${\text{桂}\subset \mathbb{Z}/9\mathbb{Z}\times\mathbb{Z}/9\mathbb{Z}}$$）、

$$
\text{桂}=\{(1,2),(-1,2)\}=\{(1,-7),(8,-7)\}
$$

が成り立つ。

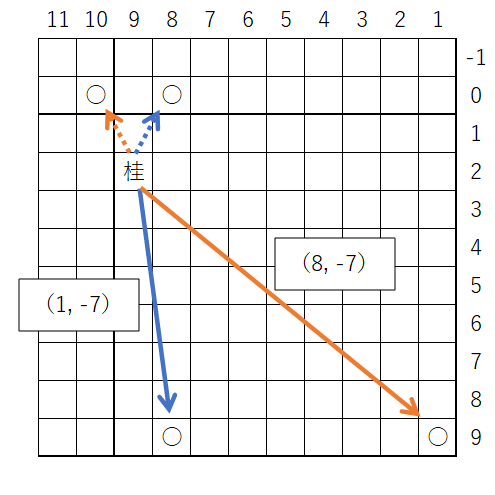
これは、トーラス盤上の桂の利きは下記のどちらの言い方をしてもよいことを意味しています。

・「右に$${1}$$、上に$${2}$$」または「左に$${1}$$、上に$${2}$$」
・「右に$${1}$$、下に$${7}$$」または「右に$${8}$$、下に$${7}$$」

ここから先の内容は今後必要になることはないと思いますが、補足として記載します。

例４.１では、無限盤上の桂をトーラス盤上の桂と見なしました。このとき数学的には何が起きているのでしょうか。

まず、$${\mathbb{Z}}$$から$${\mathbb{Z}/9\mathbb{Z}}$$への標準写像

$$
\begin{align*}
&\mathbb{Z}\longrightarrow \mathbb{Z}/9\mathbb{Z} \\
&a\;\;\mapsto \;\;a
\end{align*}
$$

があります。これを使って無限盤からトーラス盤への写像$${\pi}$$を作れます。

$$
\begin{align*}
\pi\colon&\mathbb{Z}\times\mathbb{Z}\longrightarrow \mathbb{Z}/9\mathbb{Z}\times\mathbb{Z}/9\mathbb{Z} \\
&(a,b)\;\;\mapsto \;\;(a,b)
\end{align*}
$$

上記の$${\pi}$$による駒$${A\subset\mathbb{Z}\times\mathbb{Z}}$$の像$${\pi(A)}$$が、トーラス盤上の駒$${A}$$と言えます。

一般に、写像$${f\colon X\to Y}$$と$${A\sub X}$$に対し、$${f}$$による$${A}$$の像を

$$
f(A)=\{ f(a) \mid a\in A\}
$$

と定めます。写像$${X\to Y}$$があれば、それを使って自然に別の写像$${2^X\to 2^Y}$$を作れるわけですが、どちらの写像も同じ記号で表します。

$$
\begin{align*}
f\colon X&\longrightarrow Y \\
& \\
f\colon 2^X&\longrightarrow 2^Y
\end{align*}
$$

---

次回はこちら。