揺れる雲:量子力学:Schrodinger 方程式

前回までは，調和振動子系のエネルギーを指定するハミルトニアンの固有値方程式を扱ってきた．

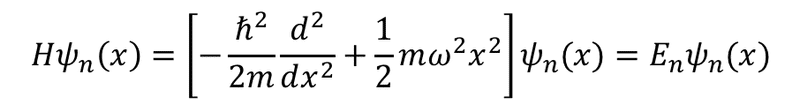
この微分と位置"x"の関数の組み合わせ[   ]を作用させるとただの数字"E_n"が返ってくるエネルギー固有関数"ψ_n"を探したのだった．

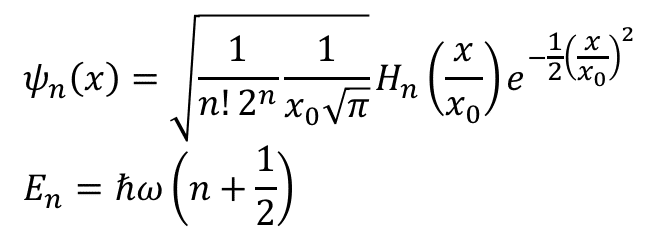
実はこの波動関数は時間を含まない関数になっている．固有値方程式を見れば，位置とその微分の微分方程式になっているのだから，これから時間"t"依存性は見つけられないのはある種当然だろう．

今日は量子力学の時間発展方程式，みんな名前は聞いたことのあるSchrodinger(シュレディンガー)方程式を紹介して，実際に解いてみよう．

Schrodinger方程式

時間と位置に依存する波動関数"ψ(x,t)"の従うSchrodingerは次のような方程式だ．

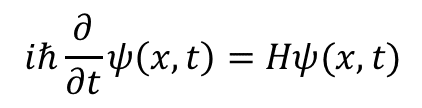
∂は(偏)微分，"i"は虚数，"h"に横棒はエイチバーと読んで量子力学に典型的にでる量だ．

左辺は波動関数の時間に対するちょびっと変化を表している．右辺はハミルトニアンがかかっている．要は時間のちょびっと変化はハミルトニアンによって生み出されるのだ．

余談
いつか話すかもしれないが，正準量子化のきっちりした手続きを踏むためには解析力学と呼ばれるものを扱わなければならない．解析力学において運動方程式は，ハミルトニアンによっても作ることができるのがわかるのだ．Schrodinger方程式は解析力学をやると，何ら特別なことはない時間発展方程式なのだとわかる．

Schrodinger方程式を解く

では実際に解いてみよう．時間に依る波動関数"ψ(x,t)"はどんな関数なのか，次のような形を想定してみよう．

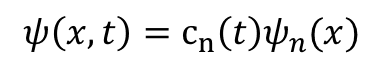
エネルギー固有関数と，何か時間の関数"c_n(t)"で書かれている場合を考えるのだ．何でこんなのを考えるかはあとでわかる．ではSchrodinger方程式にぶち込んでみよう．

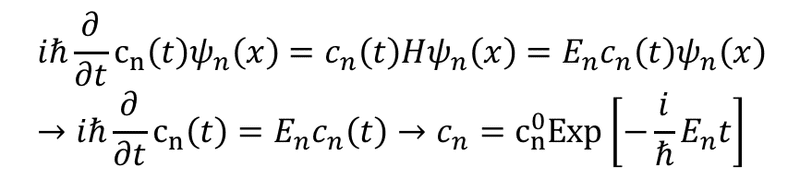
左辺の時間微分は時間の関数"c_n(t)"にだけ作用する．一方右辺は"ψ_n"はハミルトニアンの固有関数だったのだから，ただの数字"E_n"が返ってくる．ということは時間に関する微分方程式が分離できて二行目のようになる．実はこれは解いてしまえてこうなるのだ．"c^0_n"はただの数字で今回は波動関数の規格化から大きさ"1"に決められる．

やった解けた！とはならない．実はこれではものすごく特殊な状況でしか使えない．それも当然，固有関数の時間発展だけわかったのだ．

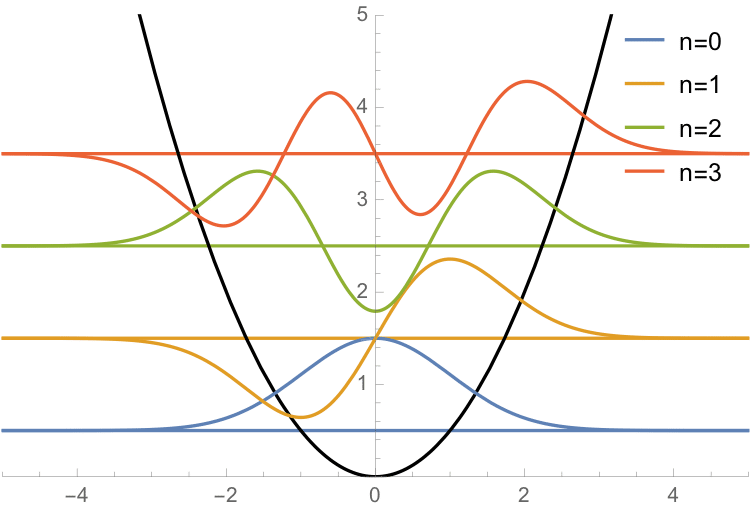
初期条件がこの絵のような超特別なセットアップの時だけ解けたのだ．

しかもこれは粒子を見出す確率密度を計算しようとすると，時間依存性が消えてしまう．エネルギー固有関数を初期条件にとると，時間によって動かないのだ．

調和振動子はバネのイメージで理解していると，エネルギーがある状態はバネが動いている時だと直感的(古典的)には思うだろう．動いていない重りはエネルギーを持たない．しかし量子力学の世界ではエネルギーが高くても全く動かない状態があるのだ．

でも現実の世界ではほとんどのものは動く．調和振動子も動いて欲しい．それは初期条件を特別な固有関数以外に取ればいいのだ．

では一般的に好きな初期条件を課した波動関数"ψ_n(x,t)"の時間発展はどうすればいいのか，それはあんまり苦労せず求められる．

実はどんな好きな(ただし量子力学の要請から規格化されている)関数を持ってきても，必ず(適当な重みをつけた)エネルギー固有関数の和で書けるのだ．

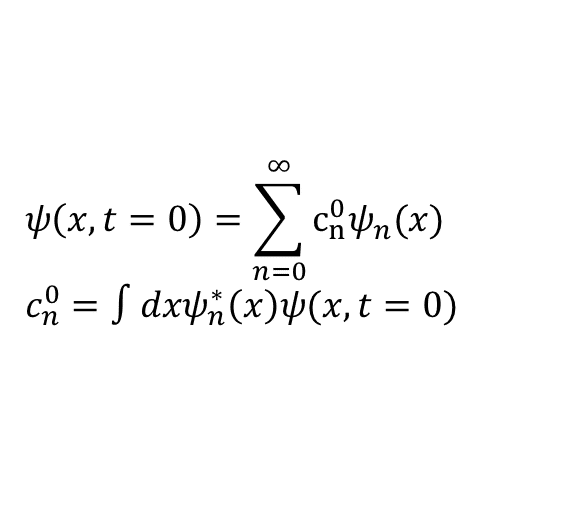
しかもその時の係数"c^0_n"は先の積分で決められる．なぜこう展開することができるかは，実は量子力学の要請からきているのだが，まぁ特別な関数なのだと思って欲しい．

こうやって好きな関数をエネルギー固有関数で展開できれば，それぞれの固有関数の時間発展を決まっているのだから，全体の時間発展が解けたことになる．

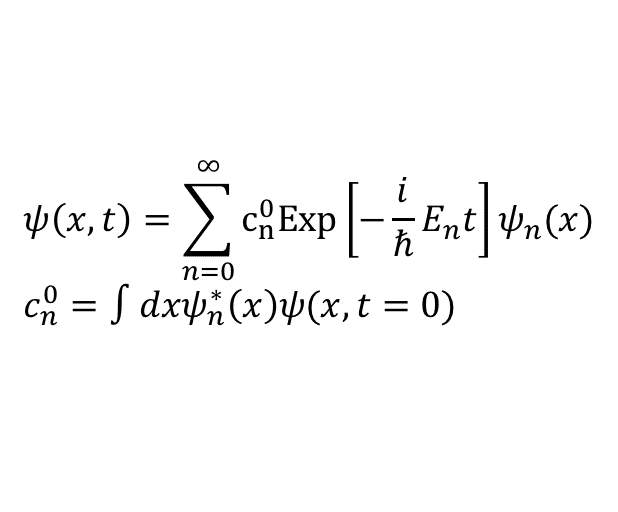
要はSchrodinger方程式はハミルトニアンの固有関数を見つけて，初期条件を固有関数で展開してしまえば，そのあとの時間発展は自ずとわかるのだ．

実例

まぁ式をいじくり回しているだけではわからないから一個実例をあげてみよう．次のような状態"ψ(x,t=0)"を考えてみよう．

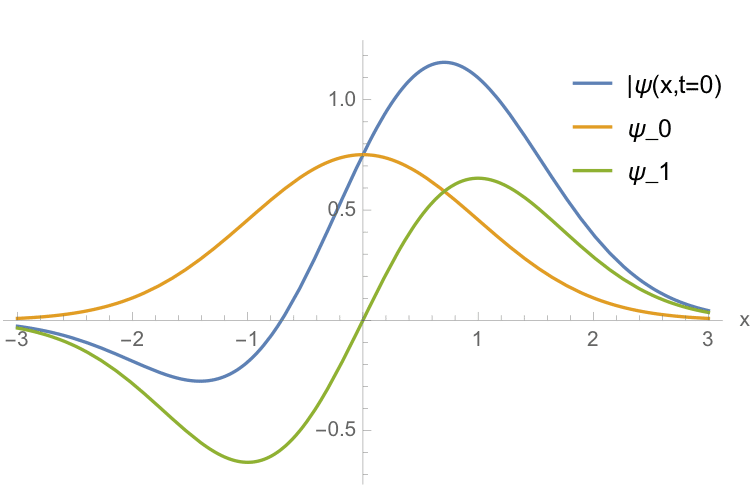
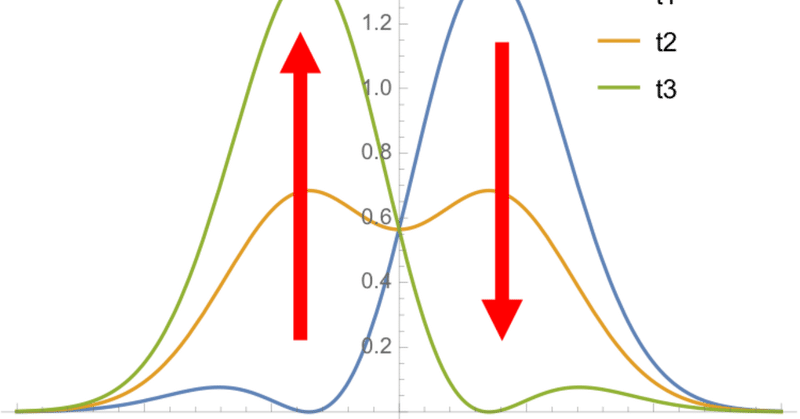
青が今回考えたい波動関数(のt=0)だ．実はこれは"n=0"と"n=1"の固有関数のただの足し算になっている．確かに青はオレンジと緑の足し算っぽい．

青を二乗したら粒子を見出す確率密度になる．マイナスは二乗すればプラスになるのだから，ふた山になりそうだ．

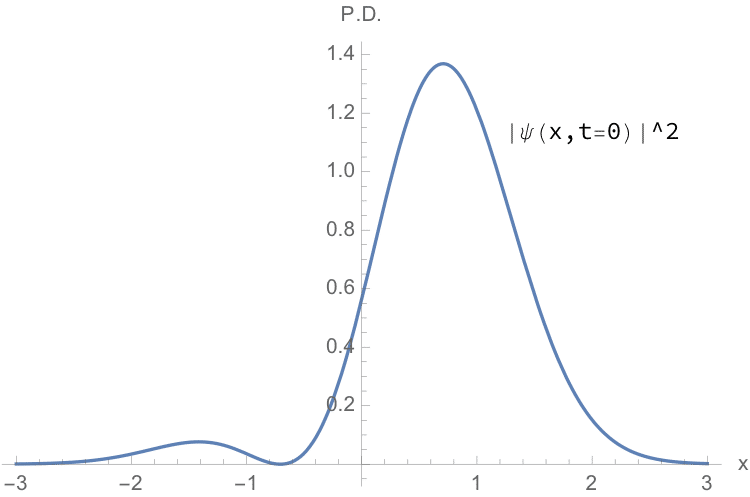
波動関数の二乗は粒子を見つける確率密度だから，これは"x=0.8"ぐらいに見つけやすい感じのふた山の分布になっている．

ではそれぞれの係数は大きさ"1"でエネルギー"E_n=\hbar ω(n+1/2)"になるのだから，さっきのSchrodinger方程式の解き方をそのまま適用して

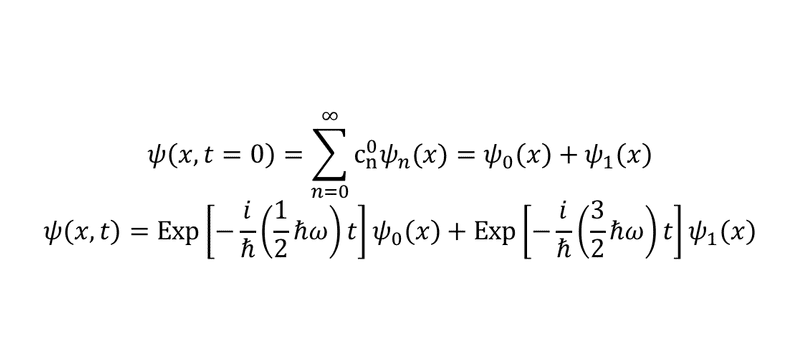
やったぜ，解けた！では数字を適当に決めて，粒子を見出す確率密度をいくつかの時間で書いてみよう．

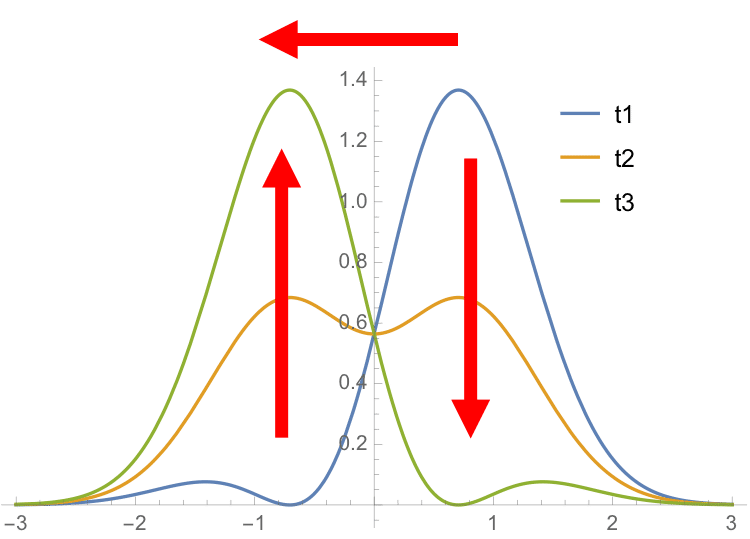
"t1"はさっきの青と同じだ．時間が経つにつれて"t2"，"t3"になっていく．こう見ると最初にあった"x>0"の山が低くなってなくなって，今度は"x<0"に山が移ったのがわかる．要は粒子を見出しやすい場所が時間によって変わったのだ．当然さらに時間が経てば，また山が"x>0"の元の位置に戻ってくる．丁度バネが振動するように量子力学でも見出す確率の高さが振動するのだ．

まとめ

・量子力学の時間発展はSchrodinger方程式によって記述される
・エネルギー固有状態は確率が時間によって動かない
・一般の初期条件はエネルギー固有状態の適当な係数をかけた和になる
・固有状態の和は時間発展によって確率が動く