私のベストテン（第10回）

(10)高坂　研 (twitter 平成30年2月14日）

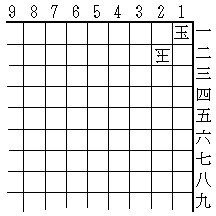
                                          持駒　sqrt(p)-leaper 1枚
                                          1手詰　2解　King Madrasi

但し、盤面は縦横とも無限に長いものとする。また、p=67280421310721であり、玉方はsqrt(p)-leaperを持っていないものとする。

King Madrasi：玉を含むすべての駒は、同種の駒から取りをかけられたとき動けなくなる。
sqrt(p)-leaper：移動距離がpの平方根に等しいリーパー。例えば、sqrt(50)-leaperは(1,7)-leaper + (5,5)-leaperである。

　まずは練習として、持駒が(2,3)-leaperだと仮定してみよう。この場合、この持駒を45或いは54に打てばそれで終わりである（玉方は同種のリーパーを持っていないし、22玉は動けない）。つまりこれは、持駒で王手をかけさえすればそれで詰むという、ある意味究極の1手詰なのだ。
　では、持駒であるsqrt(p)-leaperで王手をかけるには、どこに打てばいいのだろうか？この問いに答える為には、整数に関する予備知識が必要になる。

定理 ― 奇素数pが整数mとnを用いて p=m^2+n^2 と表されるのは、p≡1(mod 4) の時に限る。また、逆も成り立つ。そして、この分解は一意的である。

p=67280421310721は4n+1型の素数である（注1）。よって、上の定理より
p=m^2+n^2 を満たす整数 m ,n が一意に存在し、この整数m ,n を用いると与えられたリーパーは(m, n)-leaperと表すことができる（三平方の定理ですね）。従って、1手詰にする為の打ち場所は(m+2,n+2)または(n+2,m+2)であり、これ以外にないということが証明された。

　では、その m, n の具体的な数値はそれぞれいくらなのか？実を言うと、作者である私も知らないのだ。正確には、「この作品が完全作であることは保証できるが、その具体的な解は分からない」ということになる。実際に出題することはないので実害はないものの、こんなことが許されていいのだろうか？（笑）

　私の知る限り、こういった「数学の定理を詰将棋の形で表現する」ということを初めて試みたのは縫田光司氏である（注2）。氏は私と違って本物の数学者であり、その為氏の作品はどれも、フェアリー駒やフェアリールールを駆使した非常に複雑な構成になっているようだ。私にはとてもそんな高度な真似はできず、定理がそのまま解に結びつく非常に安直な表現になってしまった。まあ、無駄な装飾が一切ないという意味では、私らしいのかもしれない。

　なお、m=1やn=1があり得ない（あれば4解になってしまう）ことは中学生でも証明可能なレベルだと思うので、ここではあえて証明しない。何故それが言えるのか、読者のみなさんも一寸考えてみて下さいな。

（注1）wikipediaによると、この素数は1855年にThomas Clausenによって発見されたものらしい。

（注2）いずれもWeb Fairy Paradise（以下WFPと略す）に発表されている。興味のある方は、以下も参照してみて下さい。
・WFP 108号（ベルトランの定理）
・WFP 111号（双子素数）
・WFP 112号（巨大な合成数の素因数分解）
尚、これらは全て、以下のURLからDLできる。
www.dokidoki.ne.jp/home2/takuji/wfp.html