【機械学習】知ってるつもりの主成分分析【ＡＩ技術】

知ってるつもりになってるものを他人に解説をするつもりで整理することで理解を深めるという、完全に独り善がりなチラ裏記事。
今回は主成分分析について自分の理解を整理する。間違ってるかもしれない。少なくとも正確ではないというか厳密ではないので、読むときには参考としてください。

1.主成分分析とは

主成分分析は多変量解析手法（データ分析手法）の１つで、機械学習の枠組みでは教師なし学習に分類されているもの。

何をするものか
ざっくりいうと、多変量のデータ（カラムの多いデータセット）を少変量（カラムの少ないデータセット）のデータに集約するもの。

使用例
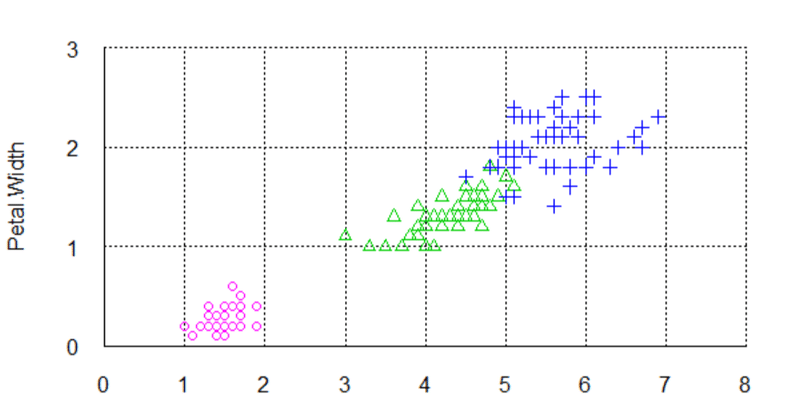
よく使われる例としては「国語」、「数学」、「理科」、「社会」、「英語」の５次元データを「総合学力」と「理系性向」に集約する。
この場合は特に主成分分析など使用せずに

「総合学力」＝「国語」＋「数学」＋「理科」＋「社会」＋「英語」
「理系性向」＝「数学」＋「理科」－「国語」－「社会」－「英語」

としても大体良さそうだけども、ある数学的な基準で下記の係数a～jを計算する。

「総合学力」＝a*「国語」＋b*「数学」＋c*「理科」＋d*「社会」＋e*「英語」
「理系性向」＝f*「数学」＋g*「理科」＋h*「国語」＋i*「社会」＋j*「英語」

何がうれしいのか
・コンピューターリソース観点としてデータ量の削減
・人からのデータ可読性が上がる（３次元までなら図表にプロットできる）
・また、データ解析の前処理として多重共線性や過学習の回避

やってることのイメージ
３次元の物体に光を当てる２次元の影絵を作り、これが何なのかを予想するクイズを考える。単純な例として木製の切り文字「Ａ」を題とする。真正面から光を当てれば「Ａ」と読める影となる一方、真横から当てると「｜」のような影ができる。これは、真正面から光を当てる場合、多くの情報量を残して３次元から２次元にデータ量を削減できたことになる。
「国語」、「数学」、「理科」、「社会」、「英語」の５次元データに対してどの方向から光を当てるといい感じの２次元に集約できるのかを数学的に計算する。

2.アルゴリズム

数式が登場する箇所は部分とても読みにくいので所々codeで記載する。記号の使い方は説明しないがlatexっぽく書いているつもり。

データセット：X = {x_{ij}} をZ = {z_{ik}} に変換する。
ここで、i=1...n, j=1...m, k=1...oとして、m > oである。
なお、Xは前処理で平均がゼロになるようにセンタリングされたものとする。
（∀j, Σ_{i} x_{ij} = 0）

主成分分析は次のプロセスで軸を探していく
・まず最も情報量を残す1次元の軸を求める
・次に１次元目の軸に垂直かつ最も情報量の多い2次元目の軸を求める
・更に１次元目、２次元目の軸に共に垂直かつ最も情報量の多い３次元目の軸を求める
．．．

2.1.最も情報量を残す1次元の軸を求める

図１は２次元風のですが、ｎ次元データのXをプロットしたものと考える。
できるだけZ軸１本でデータを表現したいので、各点ができるだけ近くなるようなZ軸をさがす。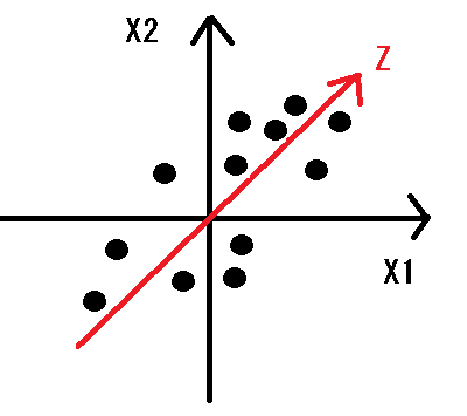

図１

1つの点x_{i}について注目して図を書き直す（図２）。
Z軸方向の長さ１のベクトルをwとして線分a_{i},b_{i},c_{i}を考え、
Σ_{i}(b_{i})^2を最小化するwを求めたい。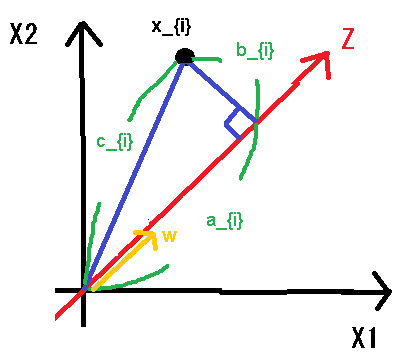

それぞれの線分の長さを考えると
  c_{i} = ||x_{i}||
, a_{i} = w^{T} x_{i} / ||w|| = w^{T} x_{i}　∵ ||w|| = 1
, b_{i}^{2} = c^{2} - a^{2}

となる。ここで Σ_{i}(b_{i})^2を最小化するwを求めたいという目的に立ち返ると、

    min_{w} Σ_{i} b_{i}^{2}
　⇔ min_{w} Σ_{i} c^{2} - a^{2}　    ∵b^{2} = c^{2} - a^{2}
　⇔ min_{w} Σ_{i} - a^{2}　　　　　    ∵c^{2}はwに依存しないので無視
　⇔ max_{w} Σ_{i} a^{2}　　　　　      ∵符号反転
　⇔ max_{w} Σ_{i}(w^{T} x_{i})^{2}　 ∵a_{i} = w^{T} x_{i}
　⇔ max_{w} w^{T} V w

ここで,V={v_{ij}}, v{ij}=x_{.i}^{T} x_{.j}, i=1...m, j=1...m
Xはセンタリングされてるので、V は X の分散共分散行列である。

まとめると解くべき問題は下記のとおり。

　　max_{w} w^{T} Vw 
　　s.t ||w||^{2}=1


ラグランジュの未定乗数法でこれを解くとV の固有値・固有ベクトルの算出式に帰着できる。

L(w) =  w^{T} Vw + λ (||w||^{2} -1 ) 
∇L(w) = 2Vw - 2λw = 0
⇔　Vw = λw

固有値・固有ベクトルはVのランク数存在するが元の目的を考えると
　w^{T}V w = λw^{T}w
　　　　  　 = λ　∵ w^{T}V = λw^{T}、||w|| = 1
を最大化したいので、最も大きい固有値λに対応する固有ベクトルが求めるwであり、
z_{i} = w^{T} x_{i} が Z軸上での評価値となる。

2.2.１次元目の軸に垂直かつ最も情報量の多い2次元目の軸を求める

x_{i} から z_{i} の情報を取り除いた x'_{i} を次のとおり定義する。

　x'_{i} = x_{i} - z_{i} w 

この x'_{i} に対して、最も情報量を残す新たなZ'軸を求める。
Z'軸方向の長さ１のベクトルをw'とすると

 z'_{i} = w'^{T}x'_{i}
        = w'^{T}x_{i} - z_{i} w'^{T}w 

Z'はZに対して垂直であることからw'^{T}w = 0なので、

 z'_{i} = w'^{T}x'_{i}
        = w'^{T}x_{i}

となる。
ということで結局１次元目の軸を求める式と同じものになるので、
２番目に大きい固有値に対応する固有ベクトルが求めるw'である。
以下３次元目も同じで、順に大きい固有値に対応する固有ベクトルを計算すればよいことになる。

3.1.おまけ
（多変量正規分布、マハラノビス距離との関連）

あらためて、各点についてj番目の軸で評価したベクトルを z_{.j} と表現し、
対応する w、λ を w_{j}、λ_{j}とする。

z_{.j} = w_{j}^{T} Vw_{j}
z_{.j}^{T} z_{.j} = w^{T} Vw = λ_{j} は z_{.j}の分散

W = [w_{1}|w_{2}|...|w_{m}] とし、
各要素がλ _{j} となる対角行列を Λ とする。


下記のとおりWは直行行列
　Vw = λwなので、VW = WΛ,  W^{-1} VW = Λ.
　w_{1}～w_{m}は長さ1で直行しているので、
　W^{T} W = I ⇔ W^{-1} = W^{T}．

対角化のテクニックで下記が成り立つ
　Λ^{n} = W^{-1} VW W^{-1} VW W^{-1}VW ・・・ 
     　 = W^{-1} V^{n} W.

証明しないが、nは自然数以外にも対応しており、
Λ^{-1/2} = W^{-1} V^{-1/2} W
　⇒　V^{-1/2} = W Λ^{-1/2} W^{-1}

　また、次のとおりV^{n}は対称行列
　V^{nT} = [ W Λ^{n} W^{-1} ]^{t}
        =  W^{-1}{T} Λ^{n} W^{T} 
 　         = W Λ^{n} W^{-1}
 　         = V^{-n}

これを使うと、Xを分散１、相関ゼロに正規化したデータZ^{*}を計算できる
　Z^{*} = V^{-1/2} X

　Z^{*}の分散共分散行列は単位行列 I なる。
　Z^{*T} Z^{*} = V^{-1/2T} X^{T} X V^{-1/2}
　　　　　　　　　 = V^{-1/2} V V^{-1/2T}
　　　　　　　　　 = I

V^{-1} = W Λ^{-1} W^{-1} 
　　　　 = W Λ^{-1/2} Λ^{-1/2} W^{-1}
　　　　 = [ W Λ^{-1/2} ] [ W Λ^{-1/2} ]^{T}
　　　　 = [ W Λ^{-1/2} ]^2

⇒　V^{-1/2}　　= W Λ^{-1/2}  

⇒　Z^{*} = V^{-1/2} X 
         = W Λ^{-1/2} X 
         = WX Λ^{-1/2}　(？あとで確認)  
         = Z Λ^{-1/2} 

なので、Z^{*} はZの標準偏差が1になるように調整されていることがわかる。
ということで、多変量正規分布やマハラノビス距離はZ^{*}上で評価した距離で
考えていることになる。

3.2.おまけその２（ラグランジュの未定乗数法）

なんとなくわかった気がして、実はよくわかってないものの代表格。
厳密なことをいうとただの数式になってしまうので、具体的なイメージで理解する。ということで、下の図を例に考える。

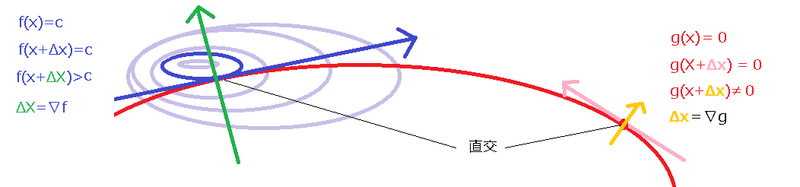
山 fを登っていきたい。f(x)を標高としてmax_{x} f(x) となるxを探したい。
ただし、歩きやすさg(x)があって、山道に沿って歩けばg(x)=0である。
危ないので山道に沿ったなかで、max_{x} f(x) となるxを探す。

解くべき問題
max_{x} f(x)　　・・・　標高が最大となるポイントを探す
s.t. g(x) = 0  ・・・　ただし、山道に沿った中で考える

g(x)=0の線上に沿って歩いたとき、どうなればそこが極値となるか？
答え）　１歩進んでも１歩下がっても標高が変わらないポイント
　　　　⇔　山道が山の等高線と平行になっているポイント
　　　　⇔　山道の接線と山の等高線の接線が並行になっているポイント

では山道の接線とは何か？
g(x)の勾配∇g(x)は歩きやすさが最も変わる方向を指す。
山道の接線は歩きやすさが全く変わらない方向を指す。
⇒　答え）山道の接線とは、勾配∇g(x)に対して直交する直線。

同様に山の等高線の接線とは何か？
f(x)の勾配∇f(x)は標高が最も変わる方向を指す。
山の等高線の接線は標高が全く変わらない方向を指す。
⇒　答え）山の等高線の接線は、勾配∇f(x)に対して直交する直線。

山道の接線と山の等高線の接線が並行になっているとは？
勾配∇g(x) と 勾配∇f(x) が並行である
⇔　∇f(x) = λ∇g(x)　である

よって、下記のとおり定式化できる

max_{x} L(x) = f(x) + λg(x)
∇L(x) = ∇f(x) + λ∇g(x) = 0 ・・・※λは±を気にしないのでたまに表記が揺れても勘弁