
動かして学ぶバイオメカニクス#7 〜オイラーの運動方程式と慣性モーメント〜
本章から逆動力学計算を利用して関節のトルクの計算について述べていく.ニュートンの運動方程式と同様で,回転の運動方程式も再帰的に解くため,必要に応じてこのシリーズの復習も行っていただければと思う.なお,今回は実際にコードを動かして確認する作業は含まれない.次のステップに向けての数学的な準備にとどまる.
回転のダイナミクス
ここで取り上げる逆動力学解析における剛体の運動方程式は,並進の運動を記述するニュートンの運動方程式(Newton's motion of equation)と,回転の運動を記述するオイラーの運動方程式(Euler's motion of equation)のセットで考える.
なお,ここで注意しておきたいことを予め述べる.回転の力学で,見落としがちなのが座標系の定義である.慣性モーメント,力のモーメント,角運動量については,これらは全てモーメントであるが,これらは座標系の原点(回転の中心)のとり方で値が異なる物理量である.
実際に計算する際には,いろいろな座標系の物理量が混在している.計算対象がどのような座標系を考えているか,常に念頭に置きながら考えていきたい.
ニュートンの運動方程式の復習
これまで述べてきた関節に作用する力を計算ではニュートンの運動方程式に基づいて計算してきた.ニュートンの運動方程式は質点の運動を記述するための運動方程式であって,いま我々が扱っているのは剛体であって質点ではない.しかし,質量中心(重心と等価)は剛体の代表点,すなわち力のモーメントが釣り合う(相殺する)点なので,剛体についても重心に関してはニュートンの運動方程式が成り立ち,重心を剛体の代表点として考えることができ,剛体の重心に対してはニュートンの運動方程式を適用することができる.
質量中心と重心に関しては
を参照していただきたい.質量中心,すなわち重心が剛体の代表点である理由も述べている.
オイラーの運動方程式
そこで,まずは関節などの幾何学的拘束がなく,トルクが作用する1つの剛体の回転の運動方程式を考えてみる(図1).
$$
\bm{I} \dot{\bm{\omega}} + \bm{\omega} \times \bm{I} \bm{\omega} = \bm{N}
$$
これをオイラーの運動方程式(Euler's motion of equation)と呼ばれる.ここで,$${\bm{I}}$$は慣性テンソル(inertia tensor), $${\bm{\omega}}$$は角速度ベクトル,$${\bm{N}}$$は剛体に作用する外力トルクベクトルである.
左辺は慣性力の項で,右辺は外力項である.左辺の第1項は,角速度ベクトルの微分,すなわち角加速度ベクトル$${\dot{\bm{\omega}}}$$と,慣性テンソル$${\bm{I}}$$はに比例した回転の慣性力で,$${ \bm{\omega} \times \bm{I} \bm{\omega}}$$は向心力項である.また,ニュートンの運動方程式において加速度$${\ddot{\bm{x}}}$$と質量$${m}$$の積が慣性力で「加速しにくさ」「運動のしにくさ」を表すのと同様に,角加速度$${\dot{\bm{\omega}}}$$と慣性テンソルの積が,回転の慣性力を構成し,「回転のしにくさ」を表す.したがって,慣性テンソルは回転方向の慣性の抵抗を意味する.
右辺の項は外力でトルク$${\bm{N}}$$は剛体を回転させる力を,すべて書き足していくことになる.
次に,このオイラーの運動方程式の導出とそれにともない慣性モーメントの定義,慣性モーメントの計測方法などについて述べていく.この導出は,読み飛ばしても構わないが,学んだことがない方は慣性テンソルの意味などを理解するため,ぜひ続けて勉強していただければと思う.
オイラーの運動方程式の導出
運動量ベクトルとニュートンの運動方程式
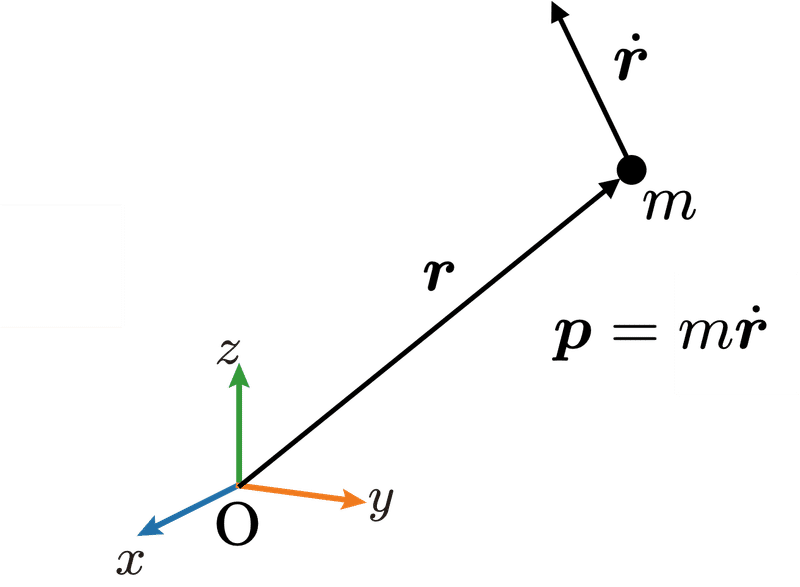
このマガジンではニュートンの運動方程式の導出は示さなかったが,オイラーの運動方程式の導出と関連するため,まずニュートンの運動方程式の導出を行う.
座標系の原点$${\text{O}}$$からみた質量$${m}$$の質点の位置ベクトルを$${\bm{r}}$$とすると(図1参照),運動量ベクトル$${\bm{p}}$$は以下のように記述でき,
$$
\bm{p} = m \frac{d\bm{r}}{dt} = m\dot{\bm{r}}
$$
これを時間$${t}$$で微分すると
$$
\dot{\bm{p}} = m \frac{d\bm{p}}{dt}= m \frac{d^2\bm{r}}{dt^2} = m\ddot{\bm{r}}
$$
を得て,右辺に外力として$${\bm{f}}$$を与えたのが,
$$
m\ddot{\bm{r}} = \bm{f}
$$
ニュートンの運動方程式である.
角運動量ベクトル
同様に回転の運動方程式を意識し,回転の運動量,すなわち角運動量ベクトル$${\bm{l}}$$を以下のように定義する.
$$
\bm{l} = \bm{r} \times \bm{p} = \bm{r} \times m \dot{\bm{r}}
$$
ここで,$${\times}$$はベクトルの外積である.外積については
を参照していただきたい.
この式は,「原点$${\text{O}}$$まわり」の質点の運動量ベクトル$${\bm{p}}$$の「モーメント」を表している.ここで,注意していただきたいことは,モーメント(慣性モーメント,力のモーメント,角運動量等)は座標系の原点の位置が変わると,値が変わる物理量ということである.座標変換すると当然モーメントの値も変化するのでモーメントも座標変換する必要がある.
モーメントについては
の補足1を参照いただきたい.

ここで,質点がある回転軸周りに角速度ベクトル$${\bm{\omega}}$$で回転運動をしている際(図2),質点の速度$${\dot{\bm{r}}}$$は
$$
\dot{\bm{r}} = \bm{\omega} \times \bm{r}
$$
となるので,質点の角運動量ベクトルは
$$
\bm{l} = \bm{r} \times \bm{p} = \bm{r} \times m \dot{\bm{r}} = m \bm{r} \times (\bm{\omega} \times \bm{r})
$$
となる.これは質点の角運動量ベクトルであるが,ここで考えるべきは剛体の角運動量であるので,剛体を$${n}$$個の質点の集合と考え
$$
\bm{L} = \sum_{i=1}^n \bm{l}_{i} = \sum_{i=1}^n \left( \bm{r}_i \times \bm{p}_i \right) \\ = \sum_{i=1}^n m \bm{r}_i \times (\bm{\omega} \times \bm{r}_i)
$$
を得る.ここで,ベクトル三重積(補足1参照)の部分は
$$
\bm{r} \times (\bm{\omega} \times \bm{r}) = [\bm{r} \times ] [\bm{\omega} \times ] \bm{r}
$$
のように書くことができる,ここで右辺の外積は歪対称行列(「わいたいしょうぎょうれつ」,または交代行列)を使用して$${[\bm{a} \times ]}$$のような記述方法を使用している.外積と歪対称行列については,
を参照されたい.なお,$${\bm{r}= [x, y, z]^T}$$とすると,歪対称行列を用いて外積は
$$
[\bm{r} \times ] = \begin{bmatrix}0&-z&y\\z&0&-x\\-y&x&0 \end{bmatrix}
$$
と書くことができ,歪対称行列の構造から
$$
[\bm{r} \times ]^T = \begin{bmatrix}0&z&-y\\-z&0&x\\y&-x&0 \end{bmatrix} = -[\bm{r} \times ]
$$
という関係を導くことができ,このことを利用し角運動量ベクトル$${\bm{L}}$$
$$
\bm{L} = \sum_{i=1}^n m_i \bm{r}_i \times (\bm{\omega} \times \bm{r}_i) \\ = \sum_{i=1}^n -m_i \bm{r}_i \times (\bm{r}_i \times \bm{\omega}) \\ ~~~~= \sum_{i=1}^n -m_i [\bm{r}_i \times ][\bm{r}_i \times ] \bm{\omega} \\ ~~~~= \sum_{i=1}^n m_i [\bm{r}_i \times ]^T[\bm{r}_i \times ] \bm{\omega}
$$
を得る.2行目では外積の交換法則が成り立たず,外積の$${\bm{a} \times \bm{b} = -\bm{b} \times \bm{a}}$$という性質から,括弧内のベクトルの順番の入れ替えに伴い負の符号がついている.それ以外は,ここで述べた性質を利用している.
ここで,$${\bm{L}}$$の中身について,もう少し詳しく眺めてみる.
剛体では質点は密度$${\rho}$$で均質に連続的に分布していると仮定すると,この離散的な式を,次のような連続的な式で表すことができる.すなわち,
$$
\bm{L} = \int_V [\bm{r} \times ]^T[\bm{r} \times ] \rho dV ~\bm{\omega}
$$
のように微小体積$${dV}$$による体積分で記述する.
そして,その中身を
$$
\bm{I} = \int_V [\bm{r} \times ]^T[\bm{r} \times ] \rho dV
$$
と置くと,角運動量ベクトル$${\bm{L}}$$は
$$
\bm{L} = \bm{I} \bm{\omega}
$$
と書くことができ,この$${\bm{I}}$$を慣性テンソル(inertia tensor)または,単に慣性行列と呼ぶ.
テンソルについて
さて,力学を学んだひともあまり気にしていないかもそれないが,なぜ,これがテンソル(tensor)という数学的表現の対象になるのだろうか?古典力学ではテンソルに関する数学的性質を使用することもほとんどないので,ここでも,ごくごく簡単に述べておく.
ここで扱う慣性テンソルは2階のテンソルで行列を使って表現する.ちなみに,0階のテンソルはスカラ,1階のテンソルはベクトルである.
したがって,行列であれば,なんでもテンソルになってしまうそうだが,テンソルは,「大きさと複数の方向に紐付けられた物理量の数学的な表現」で,単に行列で書かれていればテンソルになるわけではない.
そこで,具体的に慣性テンソルを計算することで,テンソルの意味を考える.慣性テンソルは
$$
\bm{I} = \int_V [\bm{r} \times ]^T[\bm{r} \times ] \rho dV
$$
で与えられたが,この式の積分対象の部分($${[\bm{r} \times ]^T[\bm{r} \times ]}$$)だけを取り出す.ここで,位置ベクトル$${\bm{r}_i}$$は$${\bm{r}_i = [x_i, y_i, z_i]^T}$$の成分を持つとすると
$$
[\bm{r} \times ]^T[\bm{r} \times ] = \begin{bmatrix}0&z&-y\\-z&0&x\\y&-x&0 \end{bmatrix} \begin{bmatrix}0&z-&y\\z&0&-x\\-y&x&0 \end{bmatrix}\\ ~~~~~~~~~~~=\begin{bmatrix}y^2+z^2&-x y&-x z\\-y x&z^2+x^2&-y z\\-z x&-z y&x^2+y^2 \end{bmatrix}
$$
となる.これは,単にスカラの値を並べたものではなく,前述のように$${xyz}$$の方向に紐付けられた物理量を行列に並べたものとなっている.また,慣性テンソルは
$$
\bm{L} = \bm{I} \bm{\omega}
$$
のように,角運動量ベクトル$${\bm{L}}$$と,角速度ベクトル$${\bm{\omega}}$$を結びつける役割を果たしている.
このような性質を考えると,回転行列もテンソルではと考えがちだが,これは物理量ではないのでテンソルではない.この他,テンソルには応力テンソル,電磁場のテンソルなどがある.
慣性行列(テンソル)がテンソルであることを意識させられるものの一つに,テンソルの座標変換がある.これについては後半に述べていく.この他,古典力学ではテンソルで成立する数学的性質を特に意識することも少なく,線形代数やベクトル解析により理解でごまかすことができ,中途半端な説明になったが,テンソルについてはこの程度に留めておく.ご興味ある方は,文献1などをご覧になるとよいだろう.
慣性テンソル
先程の計算結果を利用して,慣性テンソルは
$$
\bm{I} = \int_V \begin{bmatrix}y^2+z^2&-x y&-x z\\-y x&z^2+x^2&-y z\\-z x&-z y&x^2+y^2 \end{bmatrix} \rho dV \\ = \int_x \int_y \int_z \begin{bmatrix}y^2+z^2&-x y&-x z\\-y x&z^2+x^2&-y z\\-z x&-z y&x^2+y^2 \end{bmatrix} \rho dx dydz \\ = \begin{bmatrix}I_{xx}& I_{xy}& I_{xz}\\ I_{yx} & I_{yy} & I_{yz} \\I_{zx} & I_{zy} & I_{zz} \end{bmatrix}
$$
と書くことができる.ここで対角要素の
$$
I_{xx} = \int_V (y_i^2+z_i^2) dV \\ I_{yy}=\int_V (z_i^2+x_i^2) dV \\ I_{zz} = \int_V(x_i^2+y_i^2)dV
$$
は慣性モーメントと呼ばれる.また,非対角成分の
$$
I_{xy}=I_{yx} =- \int_V xy dV\\ I_{yz} = I_{zy} = -\int_V yz dV\\ I_{zx}=I_{xz} = -\int_V zx dV
$$
は慣性乗積という.
慣性テンソルは正定値対称行列となる.対称性は非対角項である慣性乗積が$${I_{xy}=I_{yx}, I_{yz}=I_{zy}, I_{zx}=I_{xz}}$$であることで示される.正定性は別途証明が必要であるが,このことは適切な座標系を選択すると,慣性乗積を$${0}$$とするような慣性テンソルにすることができることを数学的に保証している.
実際,物体の重心位置に物体に固定された座標系の原点を定めると,対称性が生まれ,座標系の軸の一つを身体の部位の長軸方向に合わせれば,非対角項である慣性乗積が$${0}$$となり,対角行列が姿勢変化に対して不変で扱いが簡単になる.このときの3つの軸を慣性主軸と呼ぶ.
すなわち身体各部の長軸方向に座標系の方向を固定すれば,非対角成分の慣性乗積は$${0}$$とみなすことができ,3つの対角成分の慣性モーメントだけで慣性テンソルを記述でき,計算上都合が良い.
また,多くの場合,身体各部位の重心位置まわりの(重心を座標系の原点と設定した場合の)慣性モーメントを使用する.なお,異なる座標系の慣性モーメントの計算は,平行軸の定理を用いて簡単に計算できる.平行軸の定理は
を参照されたい.ここでは,慣性モーメントの平行軸の定理について補足しておく.
慣性モーメントの平行軸の定理
力学計算で関係するモーメントには,慣性モーメント以外に,力のモーメント,角運動量などがある.慣性モーメントはテンソル,力のモーメントと角運動量はベクトルである.
モーメントは原点(回転の中心)のとり方で値が異なるということは,すでに述べたが,角運動量ベクトルがモーメントであることや,原点に依存して値が異なるということにも留意されたい.モーメントについては
も参照されたい.さて,

慣性モーメントも他のモーメントと同様に座標系の原点の選択によって値が異なる.また,慣性モーメントの定義から,質量$${m}$$の物体の慣性モーメントは
$$
m [\bm{r} \times ]^T[\bm{r} \times ]
$$
と書くことができることを述べてきた.
ここで,ある質量$${m}$$の剛体の重心$${\text{G}}$$まわりの慣性テンソルを$${\bm{I}_{\text{G}}}$$とする.そして,ベクトル$${\bm{r}=[x~y~z]^T}$$だけ平行移動した異なる座標系の原点$${\text{O}}$$まわりの慣性モーメントは,平行軸の定理から
$$
\bm{I}_{\text{O}} = \bm{I}_{\text{G}} + m [\bm{r} \times ]^T[\bm{r} \times ] \\ = \bm{I}_{\text{G}} + m \begin{bmatrix}y^2+z^2&-x y&-x z\\-y x&z^2+x^2&-y z\\-z x&-z y&x^2+y^2 \end{bmatrix}
$$
と書くことができる.もし,$${z}$$軸方向にだけ移動する場合は,$${\bm{r}_z=[0~0~z]^T}$$なので
$$
\bm{I}_{\text{O}} = \bm{I}_{\text{G}} + m [\bm{r}_z \times ]^T[\bm{r}_z \times ] \\ = \bm{I}_{\text{G}} + m \begin{bmatrix}z^2&0&0\\0&z^2&0\\0&0&0\end{bmatrix}
$$
となり,単に$${x,y}$$方向の慣性モーメントに$${mz^2}$$を加算すれば良いことになる.バットの慣性モーメントを計測する際,重心位置まわりの慣性モーメントを計測するよりは,グリップエンドまわりの慣性モーメントを計測するほうが都合が良いことがあるが,平行軸の定理を用いれば,バットの重心位置ばわりの慣性モーメントや,任意の位置の慣性モーメントに変換ができる.
平行軸の定理を使用する多くの場合は,新旧の原点間の距離$${l}$$と質量$${m}$$がわかれば,単に$${ml^2}$$を加算(または減算)すればよい事が多い.
慣性テンソルの座標変換
運動方程式を解く際には,身体の各部分に固定された座標系で計算することが多く,角運動量や慣性テンソルを絶対座標系で計算する必要はあまりないが,合成の角運動量の計算などでは,絶対座標系に変換する必要があるかもしれない.
ベクトルと異なり,テンソルの座標変換は回転行列は計算に使用するが,少し異なる.
絶対座標系から見た身体などのローカル(物体)座標系の回転行列を$${\bm{R}}$$とすると,絶対座標系での慣性テンソル$${\bar{\bm{I}}}$$は
$$
\bar{\bm{I}} = \bm{R} \bm{I} \bm{R}^T
$$
と書くことができる.ここで,$${\bm{I}}$$はローカル座標系での慣性テンソルである.もちろん,これは任意の座標系への変換にも適用できる.
したがって,絶対座標系での角運動量ベクトル$${\bar{\bm{L}}}$$は
$$
\bar{\bm{L}} = \bm{R} \bm{I} \bm{R}^T \bar{\bm{\omega}}
$$
となる.ここで,$${\bar{\bm{\omega}}}$$は絶対座標系からみた剛体の角速度ベクトルである.
なお,角速度ベクトルは座標系の原点のとり方には依存しないが,慣性テンソルは原点の位置に依存する物理量であることには十分注意をされたい.
オイラーの運動方程式の導出
ここでは,運動量ベクトル$${\bm{p}}$$を時間微分することでニュートンの運動方程式を導出したように,角運動量ベクトル$${\bm{L}}$$を時間微分することでオイラーの運動方程式を導出する.
なお,ベクトルで表された力学量を考える場合,慣性系と非慣性系の座標変換は,回転行列による座標変換を行えばよいだけで,ベクトルと行列で式を記述する際には座標系を意識する必要はない.
しかし,そこに回転する座標系の微分(回転行列の微分)を含む計算の場合は,絶対座標系(慣性系)と回転する物体の座標系(非慣性系)を区別して計算を行う必要がある.オイラーの運動方程式は角運動量ベクトルの時間微分から導出されるが,その過程で慣性テンソルが座標系に依存して変化し,回転行列の微分が介在するため,以下の計算では少し注意が必要である(例えば文献2のような多くの力学の教科書では「慣性系と回転系におけるベクトルの時間微分」として扱われるが,ここでは文献3にならって,補足2の歪対称行列を利用した導出を行う.本質は同じである.これらを見比べるとよい.文献4では恐らく文献3に基づいていると思われるが,同様な導出が示されているが,ニュートンの運動方程式なども丁寧に記述されている.).
ここで,絶対座標系でみた角速度ベクトルを$${\bar{\bm{\omega}}}$$としたときの,絶対座標系でみた角運動量ベクトル$${\bar{\bm{L}}}$$は
$$
\bar{\bm{L}} = \bar{\bm{I}} \bar{\bm{\omega}}
$$
となり,その時間微分は
$$
\dot{\bar{\bm{L}}} = \dot{\bar{\bm{I}}} \bar{\bm{\omega}} + \bar{\bm{I}} \dot{\bar{\bm{\omega}}}
$$
となる.この式の右辺の第1項に注目し,前節で述べた絶対座標系の慣性テンソル$${\bar{\bm{I}} = \bm{R} \bm{I} \bm{R}^T}$$から,絶対座標系の慣性テンソル$${\bar{\bm{I}}}$$の時間微分を計算すると,
$$
\dot{\bar{\bm{I}}} = \dot{\bm{R}} \bm{I} \bm{R}^T + \bm{R} \bm{I} \dot{\bm{R}}^T
$$
となるが,回転行列の微分の基本式$${\dot{\bm{R}} = [\bm{\omega} \times] \bm{R}}$$で(補足2参照)も考慮し,
$$
\dot{\bar{\bm{I}}} = ([\bar{\bm{\omega}} \times] \bm{R}) \bm{I} \bm{R}^T + \bm{R} \bm{I} ([\bar{\bm{\omega}} \times] \bm{R})^T \\ = [\bar{\bm{\omega}} \times] \bm{R} \bm{I} \bm{R}^T + \bm{R} \bm{I} (\bm{R}^T [\bar{\bm{\omega}} \times]^T ) \\ =
[\bar{\bm{\omega}} \times] \bar{\bm{I}} + \bar{\bm{I}}[\bar{\bm{\omega}} \times]^T \\ =
[\bar{\bm{\omega}} \times] \bar{\bm{I}} - \bar{\bm{I}}[\bar{\bm{\omega}} \times]
$$
となり,これを前述した慣性テンソルの時間微分の式($${\dot{\bar{\bm{L}}} = \dot{\bar{\bm{I}}} \bar{\bm{\omega}} + \bar{\bm{I}} \dot{\bar{\bm{\omega}}}}$$)に代入すると
$$
\dot{\bar{\bm{L}}} = [\bar{\bm{\omega}} \times] \bar{\bm{I}} \bar{\bm{\omega}} - \bar{\bm{I}}[\bar{\bm{\omega}} \times]\bar{\bm{\omega}} + + \bar{\bm{I}} \dot{\bar{\bm{\omega}}}
$$
を得る.ここで,$${[\bar{\bm{\omega}} \times] \bar{\bm{\omega}} = [\bar{\bm{\omega}} \times]^T \bar{\bm{\omega}} = \bm{0}}$$(同じベクトル同士の外積は$${0}$$)なので,角運動量の時間微分は
$$
\dot{\bar{\bm{L}}} = [\bar{\bm{\omega}} \times] \bar{\bm{I}} \bar{\bm{\omega}} + \bar{\bm{I}} \dot{\bar{\bm{\omega}}}
$$
となる.そこで角運動量の時間微分,すなわち回転の運動方程式
$$
\frac{d}{dt}(\bm{L}) =\frac{d}{dt}(\bm{I} \bm{\omega}) = \bm{N}
$$
は
$$
\bm{I} \dot{\bm{\omega}} + \bm{\omega} \times \bm{I \omega} = \bm{N}
$$
のようになる(文献3参照).最後の式は,$${\bm{N}}$$は剛体に作用する外力トルクベクトルである.ここでは,もはや座標系の選択とは無関係に成り立っている.
慣性モーメントの計測
身体の慣性モーメントを実測することは困難なので,身体各部の質量と同様に統計モデルを用いて計算することになる.しかし,もしバットやゴルフクラブなどを持って場合の力学解析を行う場合,質量は簡単に計測できるが,道具の慣性モーメントを取得する際には慣性モーメントの計測を行うか,計算を行うしかない.
均質な構造なら,形状から計算することは可能である.それらは力学のの教科書をご覧になるとよいだろう.積分ができればよい.しかし,ボールのような球体でも,内部構造や密度分布を決めるのは容易ではない.結局,計測を行う必要性がでてくる.
計測方法については,別途述べていくことにする.エッセンスだけ述べておくなら,基本的には重力加速度を既知の定数として,振動の力学を用いることになる.大学の物理実験では既知の慣性モーメントの振動を利用して,高精度に重力加速度を同定するという実験を行うが,単にその反対の計算を行うだけである.そのとき平行軸の定理も活用する.
次章について
次章
では,
で使用した,身体各部の質量や重心を計算するモデルを用いて,同様に慣性モーメントの算出方法について述べていく.
補足
補足1:ベクトル三重積
ベクトル三重積
$$
\bm{a} \times (\bm{b} \times \bm{c}) = [\bm{a} \times ] [\bm{b} \times ] \bm{c} \\ = (\bm{a}^T \bm{c})\bm{b} - (\bm{a}^T \bm{b})\bm{c}
$$
は任意のベクトル$${\bm{c}}$$に対して成り立つと考えると,
$$
\bm{ba}^T -(\bm{a}^T \bm{b}) \bm{E}
$$
が成り立つ.ここで$${\bm{E}}$$は単位行列である.このことを利用すると,ベクトル三重積は
$${\bm{a} \times (\bm{b} \times \bm{c}) = [\bm{a} \times ] [\bm{b} \times ] \bm{c} \\ = (\bm{a}^T \bm{c})\bm{b} - (\bm{a}^T \bm{b})\bm{c} \\ = (\bm{a}^T \bm{c})\bm{b} - (\bm{c} \bm{a}^T)\bm{b}}$$
と書き換えることができる.
補足2:回転行列の微分
回転行列$${\bm{R}}$$は,正規直交基底を並べた直交行列である.回転行列の性質は
などを参照していただきたい.直交行列とは,転置行列が逆行列となる,すなわち
$$
\bm{R}^T = \bm{R}^{-1}
$$
を満たす行列である.$${\bm{R}}$$が回転行列であることに立ち返ると,逆回転が$${\bm{R}^{-1}}$$だが,それは転置行列$${\bm{R}^T}$$と等しいということを述べている.なお,
$$
\bm{A} = \begin{bmatrix} a&b&c \\ d&e&f \\ g&h&i \end{bmatrix}
$$
とすると,その転置は
$$
\bm{A}^T = \begin{bmatrix} a&d&g \\ b&e&h \\ c&f&i \end{bmatrix}
$$
となる.このような非対角項を,対角項を境に入れ替えた行列を転置行列と呼ぶ.
すると以下の式が成り立つ.
$$
\bm{RR}^T = \bm{R}^T \bm{R} = \bm{E}
$$
ここで,$${\bm{E}}$$は単位行列である.回転行列$${\bm{R}}$$に逆回転$${\bm{R}^{-1}=\bm{R}^T}$$をかけると,順序を逆にしてももとに戻るという意味である.そこで,この式を時間微分することで,
$$
\dot{\bm{R}} \bm{R}^T + \bm{R} \dot{\bm{R}}^T = \bm{0}
$$
が成り立つ.左辺の2つ項は転置関係にあり,
$$
\dot{\bm{R}} \bm{R}^T + (\dot{\bm{R}} \bm{R}^T)^T = \bm{0}
$$
と同じである.そこで,$${\bm{\Omega} = \dot{\bm{R}} \bm{R}^T}$$と置き換えると,
$$
\bm{\Omega} + \bm{\Omega} ^T = \bm{0}
$$
を満たす.このような条件を満たす,$${\bm{\Omega}}$$は$${\bm{\Omega}}$$が次のような歪対称行列(交代行列)
$$
\bm{\Omega} =
\begin{bmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{bmatrix}
$$
となる(そもそも歪対称行列の定義が$${\bm{A}= -\bm{A}^T}$$を満たす行列である).すると$${\bm{\Omega}}$$は外積を表す歪対称行列と同じなので
$$
\bm{\Omega} = [\bm{\omega} \times ] =
\begin{bmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{bmatrix}
$$
のように書くことができる.また,
$$
\begin{aligned}
\bm{\Omega} &= -\bm{\Omega} ^T
\\
\dot{\bm{R}} \bm{R}^T &= -\bm{R} \dot{\bm{R}}^T
\\
\dot{\bm{R}} &= (-\bm{R} \dot{\bm{R}}^T)\bm{R}
\\
&= [\bm{\omega} \times] \bm{R}
%\\
%&= \bm{\Omega}\bm{R}
\end{aligned}
$$
であるため,この結果を利用すると
$$
\bm{\Omega} = [\bm{\omega} \times ] = -\bm{R} \dot{\bm{R}}^T = \dot{\bm{R}} \bm{R}^T
$$
を得る.
参考文献
1)物理のためのベクトルとテンソル,ダニエル・フライシュ著,岩波書店,2013
2)力学読本,自然は方程式で語る,大島著,名古屋大学出版会,2012
3)ロボットモーション(岩波講座ロボット学2),内山,中村著,岩波書店,2004
(この書籍はすでに絶版となっているようだが,回転の運動学,力学を学ぶには貴重な書籍である.図書館などで見かけられたらぜひ借りてみては.)
4)ロボットと解析力学(ロボティクスシリーズ10),有本,田原,コロナ社,2018

【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
