モーションにおける3次元回転 #9 〜3次元回転・公式集〜
最近では,モーションセンサやモーションキャプチャの出力も単位クォータニオンの出力が標準になりつつあり,3次元回転を扱うには単位クォータニオンの理解が不可欠である.
そこで,ここまで述べてきた3次元回転の式を単位クォータニオンによる表現を中心に以下にまとめる.
3次元回転を理解する上でオイラー角の理解も必要ではあるが,実際の計算では,ここで述べてきた単位クォータニオンのベクトルや行列表現に慣れることで,3次元回転の幾何学的な理解を深めたり,より効率良い計算を実行できる.
また,3次元回転の理解のためには,この章ではまとめを割愛したが1,2章で述べた回転行列の正規直交基底,方向余弦行列としての幾何学的理解,直交行列としての数学的理解も不可欠である.
数学の基礎
ベクトルと行列
ここでは(通常),ベクトルは縦ベクトル
$$
\bm{a}=\begin{bmatrix} a_1\\a_2\\a_3 \end{bmatrix}
$$
で表す.ただし,紙面の関係で$${\bm{a}=[a_1~a_2~a_3 ]^T}$$のように横ベクトルの転置で記述することがある.
ここで,右上付きの記号は$${T}$$,行列の転置を表し,
$$
\begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}
\end{bmatrix}^T
=
\begin{bmatrix} a_{11} & a_{21} & a_{31}\\ a_{12} & a_{22} & a_{32}\\ a_{13} & a_{23} & a_{33}
\end{bmatrix}
$$
のように行列の非対角要素($${a_{ij}, i\neq j}$$)を入れ替える.
したがって,最初に示した横ベクトルの転置($${\bm{a}=[a_1~a_2~a_3 ]^T}$$)で記述したベクトルも縦ベクトルである.
ベクトルの内積
ベクトル$${\bm{b}=[b_1~b_2~b_3]^T}$$と$${\bm{c}=[c_1~c_2~c_3]^T}$$の内積は$${b_x c_x+b_y c_y+b_z c_z}$$であるため,これは
$${{{\bm{b}}^T \bm{c}}= \begin{bmatrix}b_x&b_y&b_z\end{bmatrix}\begin{bmatrix}c_x\\c_y\\c_z\end{bmatrix}= b_x c_x+b_y c_y+b_z c_z}$$
のように横ベクトルと縦ベクトルの積で記述できる.ここでは,ベクトルの内積をこの方法で記述する.
ベクトルの外積
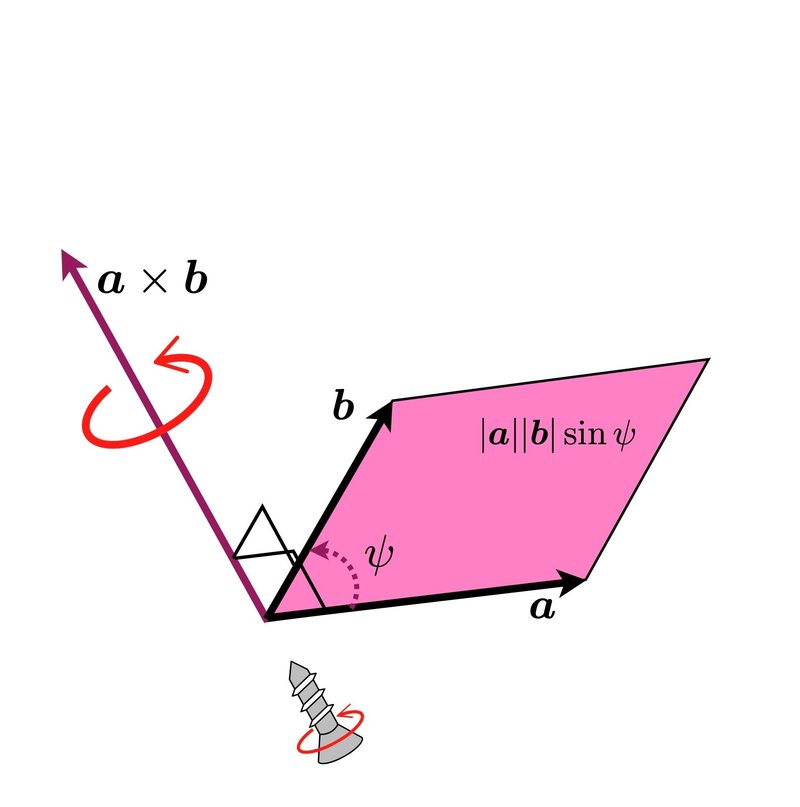
ベクトル $${\bm{a}}$$と$${\bm{b}}$$の外積$${\bm{a} \times \bm{b}}$$は,図1のように,2つのベクトル$${\bm{a}, \bm{b}}$$に対して垂直な方向のベクトルを定め,その大きさは$${\bm{a}, \bm{b}}$$がつくる作る平行四辺形の面積に等しい.
また,2つのベクトル
$${\bm{a}=\begin{bmatrix}a_x\\a_y\\a_z\end{bmatrix}, \bm{b}=\begin{bmatrix}b_x\\b_y\\b_z\end{bmatrix}}$$
に対して,外積は
$${\bm{a} \times \bm{b}=\begin{bmatrix}a_y b_z - a_z b_y\\a_z b_x - a_x b_z\\a_x b_y - a_y b_x\end{bmatrix}}$$
となる.
外積の行列表現
ベクトル$${\bm{n}=[n_1~n_2~n_3]^T}$$をつかった外積の歪対称行列表現
$${[\bm{n} \times] \equiv \begin{bmatrix}0&-n_3&n_2\\n_3&0&-n_1\\-n_2&n_1&0\end{bmatrix}}$$
を利用し,外積演算$${\bm{a} \times \bm{b}}$$を
$$
\bm{a} \times \bm{b} = [\bm{a} \times] \bm{b} =
\begin{bmatrix}0&-a_3& a_2\\ a_3&0&-a_1\\-a_2&a_1&0\end{bmatrix}
\begin{bmatrix}b_1\\ b_2\\b_3\end{bmatrix}
$$
と書くことができる.
3次元回転
ロドリゲスの式
オイラーの定理:剛体の任意の3次元回転は,一つの回転軸と回転角度で表すことができる.
一つの回転軸$${\bm{n}}$$と回転角度$${\psi}$$で表現した回転行列(ロドリゲスの式)
$$
\bm{R}_{\bm{n}}(\psi)=e^{[\bm{n}\times]} = \bm{E} + [\bm{n} \times ] \sin \psi + [\bm{n} \times ]^2(1- \cos \psi)
\qquad\qquad(1)
\\~
\\
=\left[\begin{array}{cc}\cos\psi + n_x^2(1-\cos\psi) & n_x n_y(1-\cos\psi)-n_z \sin \psi \\ n_y n_x(1-\cos\psi)+ n_z \sin \psi & \cos\psi + n_y^2(1-\cos\psi) \\ n_z n_x(1-\cos\psi) - n_y \sin \psi & n_z n_y(1-\cos\psi) + n_x \sin \psi \end{array}\right.\\ ~\\ \hspace{6cm} \left.\begin{array} {c}n_x n_z(1-\cos\psi) + n_y \sin \psi\\ n_y n_z(1-\cos\psi) - n_x \sin \psi\\ \cos\psi + n_z^2(1-\cos\psi)\end{array}\right]
~~(2)
$$
ロドリゲスの式の単位クォータニオン表現
(単位クォータニオンについては後述)
$$
\bm{R}(q_0, \bm{v}) = (2 q_0^2-1)\bm{E} + 2 (\bm{v}\bm{v}^T + q_0 [\bm{v} \times])
\qquad\qquad(3)
$$
ロドリゲスの式の逆変換 (回転行列 → 回転軸と回転角度)
回転行列$${\bm{R}}$$を
$$
\bm{R}=\begin{bmatrix}n_{11}&n_{12}&n_{13}\\ n_{21}&n_{22}&n_{23}\\ n_{31}&n_{32}&n_{33}\end{bmatrix}
$$
とし,ベクトル$${\bm{w}}$$を
$$
\bm{w}\equiv\begin{bmatrix}n_{32} - n_{23}\\ n_{13} - n_{31} \\ n_{21}-n_{12}\end{bmatrix}
$$
と定義すると,回転軸$${\bm{n}}$$と回転角度$${\psi}$$は
$$
\bm{n}=\frac{\bm{w}}{||\bm{w}||}
\qquad\qquad\qquad(4)
$$
$$
\psi = \mathrm{atan2} (\sin \psi, \cos \psi)
\qquad\qquad(5)
$$
となる.ここで
$$
\cos \psi = \frac{1}{2}(\mathrm{tr}~ \bm{R} - 1)\\ = \frac{1}{2}(n_{11} + n_{22} + n_{33}-1)
$$
トレース$${{\mathrm{tr}}~ \bm{R} = n_{11} + n_{22} + n_{33}}$$は,行列$${\bm{R}}$$の対角要素の和
$${\sin \psi}$$はロドリゲスの式$${\bm{R} = \bm{E} + [\bm{n} \times ] \sin \psi + [\bm{n} \times ]^2(1- \cos \psi)}$$から算出.
単位クォータニオン
単位クォータニオンはオイラーパラメータと数学的には等価であり,ここでは
$$
\bm{q}=\begin{bmatrix}
\cos \frac{\psi}{2} \\ \bm{n}\sin \frac{\psi}{2}
\end{bmatrix}=
\begin{bmatrix}
\cos \frac{\psi}{2} \\ n_1 \sin \frac{\psi}{2} \\ n_2 \sin \frac{\psi}{2} \\ n_3 \sin \frac{\psi}{2}
\end{bmatrix}
=\begin{bmatrix}
q_0\\q_1\\q_2\\q_3
\end{bmatrix}
=\begin{bmatrix}
q_0\\ \bm{v}
\end{bmatrix}
\qquad(6)
$$
と表す.ここで,$${q_0}$$はスカラー部,$${\bm{q}=[q_1~q_2~q_3]^T}$$はベクトル部で,$${\psi}$$は回転角度,$${\bm{n}}$$が回転軸に相当する.また,$${\bm{n}}$$は($${||\bm{n}||=\sqrt{n_1^2+n_2^2+n_3^2}=1}$$:ノルムが1)の単位ベクトルである.
単位クォータニオンの性質
1.クォータニオンのノルム
$$
||\bm{q}|| = \sqrt{\bm{q} \bm{q}^{*}}= \sqrt{\bm{q}^{*}\bm{q}} = \sqrt{q_0^2 + q_1^2 + q_2^2 + q_3^2}
$$
単位クォータニオンに関しては$${\bm{n}}$$が大きさ1の単位ベクトルであるので,
$$
||\bm{q}|| = q_0^2+q_1^2+q_2^2+q_3^2 = 1
$$
2.共役クォータニオン$${\bm{q}^{*}}$$
$$
\bm{q}^{*}=q_0-q_1 - q_2 j - q_3 k=q_0 - \bm{v} = \begin{bmatrix}
q_0\\-q_1\\-q_2\\-q_3
\end{bmatrix}
$$
単位クォータニオンの共役のノルムも
$$
||\bm{q}^*|| = q_0^2+(-q_1)^2+(-q_2)^2+(-q_3)^2 = 1
$$
3.クォータニオンの逆元(逆クォータニオン)
$$
q^{-1} = \frac{q^{*}}{||q||^2}
$$
単位クォータニオンの逆元は共役単位クォータニオン
$$
q^{-1} = q^{*}=\begin{bmatrix}q_0\\-q_1\\-q_2\\-q_3\end{bmatrix}
$$
4.無回転の単位クォータニオン:identity quaternion$${\bm{1}}$$(太文字の1)
$${\bm{1}=\begin{bmatrix}1\\0\\0\\0\end{bmatrix}}$$
5.単位クォータニオンの全要素の符号の反転は,反対の回転軸と反対方向の回転角度を意味するので,結果,同一の回転を意味する(単位クォータニオンの冗長性).
クォータニオン積
ここから先は
¥ 100
