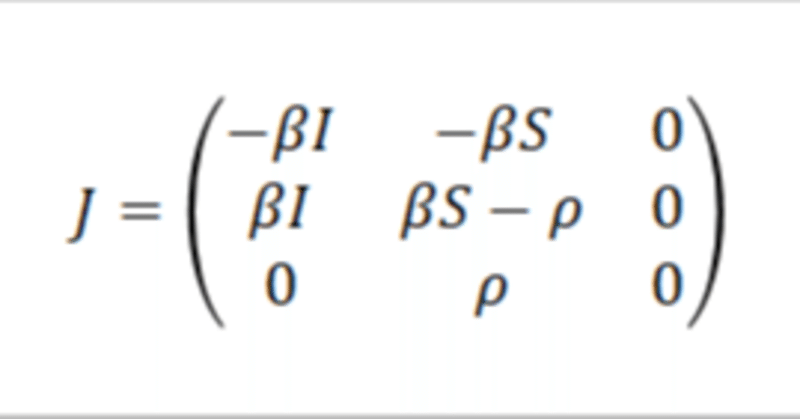
SIRモデル・SZRモデルの数的解析　ある時点におけるゾンビの感染拡大可能性を調べる（後編）

ひとつ前の記事と前編はこちら

前編のおさらい

前編では、SZRモデルを連立微分方程式に書き換え、そこからヤコビ行列を作るところまでを行った。この過程を、SIRモデルを使っておさらいしてみよう。

まず、SIRモデルは下図の通りだ。

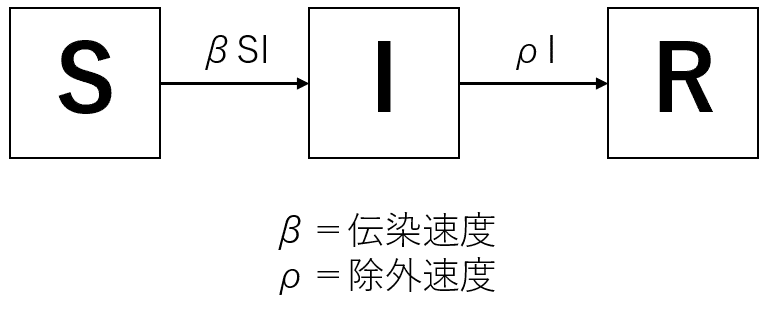
ここから一気にS、I、Rについての連立微分方程式を作ってみよう。式は次の通りだ。

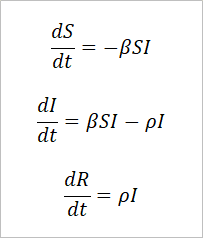
さて、連立微分方程式ができたら次はヤコビ行列だ。ヤコビ行列を作るときは、S、I、Rに何をしたら(dS/dt)、(dI/dt)、(dR/dt)になるのか考えればよいのだった。SIRモデルでも、SZRモデルと同様に何か文字式をかければよさそうだ。
ところで、時間微分（対象がある時間にどのくらい増えたか）を表す(d/dt)には慣れてもらえただろうか。

さあ、SIRモデルのヤコビ行列は次の通りになる。行列の中身は上から順に(dS/dt)、(dI/dt)、(dR/dt)への変換で、左から順にS、I、Rからの変換を表している。たとえば、左上はSから(dS/dt)への変換で、真ん中はIから(dI/dt)への変換だ。

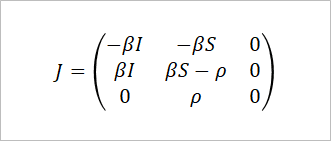
モデルから連立微分方程式を作る、連立微分方程式からヤコビ行列を作る。SIRモデルやSZRモデルでは比較的簡単だが、他のモデル（SIZRモデルや治癒あり、隔離ありモデルなど）でヤコビ行列を作ろうとすると、要素が4つ5つに増えるので、少々厄介かもしれない。
しかし、とにかく手を動かさないと計算は身につかないので、たくさん試していただきたい。

というところで前編のおさらいを終了する。

ヤコビ行列から何を知りたいのか

ヤコビ行列を作ったが…だからなんだというのだろうか。ヤコビ行列がゾンビパンデミックのシミュレーションの何の役に立つというのか。そもそも何を知りたくて数的解析を進めていたのだっけか。

前編冒頭には、「ある時点において人間やゾンビが増えるか減るかを議論できるようにしたい」と書いた。これが初心だ。
そして…Rは気にしていなかったようなので今後はあまり言及しないことにしよう。

人間やゾンビ、つまりSやZのことだが、これらが増える、減る、増減しないというのはどういうことなのか。せっかく時間微分を導入したのだから、これを使って数学的に説明していこう。
たとえば、(dS/dt)とは時間当たりのSの増加量だった。これをはじめは「一日当たりの人間（非感染者）の増加量」と呼んでいた。つまり、ある時点でSであれば、次の時点ではS+(dS/dt)になっているということだ。ゆえに、(dS/dt)=0のときSは増減しない。また、(dS/dt)>0のときSは増加し、(dS/dt)<0のときSは減少する。

したがって、ある時点において増減を議論するためには、その”ある時点”でのS、Z、Rの時間微分の値を検証するのが有効だと言える。ただし、ある時点での時間微分の値がゼロであっても次の瞬間に正か負の値をとることもあるだろう（隔離/治療ありSIZRモデルなど）。
しかしたとえば、SZRモデルのシミュレーションが進んで人類が滅亡して以降はSもZも増減することはなかった。このようなS、Z、Rの値の組み合わせは平衡解と呼ばれ、そこからシミュレーションを進めてもその値から変化するはない。

つまり、時間微分の値は時間微分方程式に値を代入すればわかるが、それだけでは足りない。ある時点におけるS、Z、Rの値が平衡解となるかどうかが重要だ。これを求めるにはどうすればよいのか。

ヤコビ行列の固有値を求める

平衡解かどうか知りたいときには、ヤコビ行列の固有値を求めるとよい。まず、固有値の前に固有ベクトルについて説明しよう。

何度も述べるが、行列はベクトルを変換するものだ。ベクトルに行列をかけると別のベクトルになる…というのが変換なのだが、変換後のベクトルが変換前のベクトルの定数倍になっていることがある。以下に具体例を示そう。

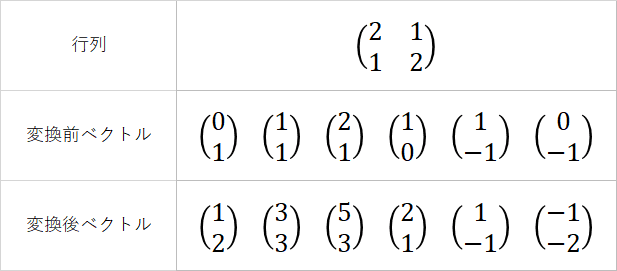
上記図で示した行列で、変換前ベクトル6つを変換すると、それぞれ変換後ベクトル6つになる（計算すればわかる）。ところで、左から2つ目のベクトル（1, 1）と右から2つ目のベクトル（1, -1）を見ると、それぞれ（3, 3）と（1, -1）に変換されている。
（3, 3）は3×（1, -1）で、（1, -1）は1×（1, -1）と表せる。この関係は具体例の直前に述べた、「変換後のベクトルが変換前のベクトルの定数倍」そのものだ。もうちょっとわかりやすく言葉で書き下すと次のようになる。

（行列）×（変換前ベクトル）
＝（変換後ベクトル）
＝（定数）×（変換前ベクトル）

ある行列に対してこのような性質を持つベクトルは固有ベクトルと呼ばれる。また、変換されるときにかける定数（ここでは3と1）は固有値と呼ばれる。つまり、上記式は次のように書き換えられる。

（ある行列）×（固有ベクトル）＝（固有値）×（固有ベクトル）

さて、肝心の固有値の求め方だが…各々調べていただきたい。「固有値　求め方」や「固有方程式」あたりで検索をすれば出てくるはずだ。原理まで理解しようとするとかなり難しいので、まずは固有値の導出・計算方法だけ身につけてほしい。どうせ原理なんて数学ガチ勢にくらいしか必要ないし…。面白いんだけどさ。
ところで、SZRモデルのヤコビ行列は具体例のような数字だけの行列ではなく、文字式のみで構成された行列だ。しかしそれでも計算法がわかれば安心。固有値が文字式で出てくるだけなのだから。

それでは本題に入ろう。文字式で得られたSZRモデルの固有値にパラメータα、βやある時点でのS、Zを代入すれば、固有値の具体的な値がわかる。また、固有方程式は高次方程式なので、固有値は2つ以上出るし、複素数になることもある。

そうして固有値を調べると何がうれしいのか。
もちろん、ある時点の固有値を調べると、安定性（平衡解かどうか）がわかるのである。ヤコビ行列から作った固有値には、以下の特性がある。

①ひとつでも複素数の実部が正なら『不安定』
②すべての実部が負かゼロなら『漸近的安定』
③すべての実部がゼロで虚数のみならば『安定』

なぜそうなるかは今回は省略する。不安定、漸近的安定、安定について、以下にざっくり説明する。

『不安定』とは、その時点の値（たとえばS、Z、R）は平衡解ではなく、必ず値は変化することを意味する。SZRモデルのシミュレーションにおいては、計算を始めた初期の段階が不安定にあたるだろう。Sは急激に減少し、Zは急激の増加するのだから。
『漸近的安定』とは、その時点の値が平衡解であり、シミュレーションはそこへ向かって進行することを意味する。これはシミュレーションを進めて、人類が滅亡して以降に相当する。
『安定』とは、その時点の値は平衡解であるが、シミュレーションはその値を中心に揺れ動いて一点に落ち着かないことを意味する。残念ながらSZRモデルではお目にかかることはできないが、たとえば温度調整をしているとき、うまくいかずに目的の温度を中心に上がったり下がったりするのがこれに当たる。

これらは「時間をパラメータとした相平面」を描けばもっとわかりやすいのだが…また別の記事で説明することにしよう。

SZRモデル検証　人類の生存と滅亡

さて、ヤコビ行列の固有値について解説も済んだところで、具体的にSZRモデルを解析していこう。ここから先、人類の生存と滅亡について2つの可能性を検討する。もちろん、ご存知の通り人類は滅亡するのだが。
SZRモデルの検証なので、使うヤコビ行列は下記式の通りだ。ヤコビ行列を表す文字Jの後の（S, Z, R）は変数、つまり代入すべき値を表す。Rに代入先はないけど…。

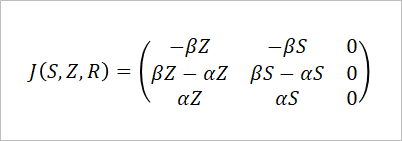
まずは人類生存について検討する。
これまでのシミュレーションはすべてS=9999、Z=1、R=0で始めていた。早速この値をヤコビ行列に代入しよう。

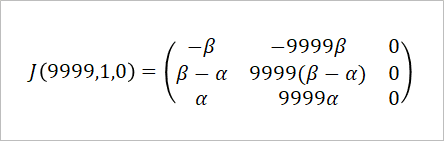
このヤコビ行列の固有方程式を解いて固有値λを求める。固有方程式を計算すると、固有値λは次の3つの値をとる。

λ=0, -β, 9999(β-α)

βとαは常に正の実数なので-β<0である。9999(β-α)はβとαの大小関係によって正負が決まる。すなわち、以下の結論が導き出される。

β>αのとき、固有値のひとつが正となるので、（9999, 1, 0）は不安定。つまり、人類生存は絶望的
α≧βのとき、固有値がすべて負あるいは0となるので、（9999, 1, 0）は安定。つまり、人類は生存する

また、以上の議論はSが9999でなくとも成り立つ。というより、SとZがゼロでない限りは必ず上の固有値の議論が成り立つ。S=9999とZ=1の値を変更すればいいだけなので。人類が生存している限り、人類の生存は安定な解ではないのだ。なんとも皮肉な。
ちなみに、ゾンビ1体を破壊して（9999, 0, 1）になったときでも、β>αであれば不安定となる。なんでかなあ。

次に、人類滅亡について検証する。
人類が滅亡したときの値を代入して、その安定性を見てみよう。人類が滅亡したのでS=0だが、ゾンビと死体の数はわからないのでそれぞれ文字でZ1とR1と置くことにする。このとき、ヤコビ行列は以下の通りになる。

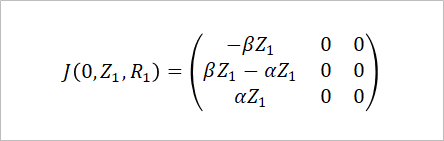
このヤコビ行列の固有値を求める。

λ=0, 0, -βZ1

前述の通りβ>0で、かつZ1>0なので、固有値は常に0か負である。固有値は正にはなりえない。したがって、（0, Z1, R1）は常に漸近的安定。つまり、シミュレーションは人類滅亡に向かって進んでいくと言える。

まとめ

SZRモデルからヤコビ行列を作り、固有値を求めてある時点の安定性を調べた。

βとαの大小関係によって人類の生存が安定かどうか決まるという結論は、前回の記事と全く同じだ。だが、固有値を使うことでS>0である限りは不安定で、S=0のときのみ漸近的安定だということがわかった。これはシミュレーションを進めると、自然にS>0からS=0へ移行することを意味する。
このように、初期状態および起こりうるシミュレーション結果におけるヤコビ行列の固有値を確かめることで、シミュレーションの過程全体を追うことが可能なのだ。これが強みだ。

また、今回は3x3の行列で済んだが、SIZRモデルや隔離ありSIZRモデル（SIZR+Q）では4x4、5x5のヤコビ行列の固有方程式を解かねばならない。基本的に頑張って計算すれば解ける。今回はこれ以上頑張りたくないので、計算はせずにここで終わる。ただ、P.Muntzらの論文では5x5は何やら工夫して解いていた。引用文献を読んだら、そちらの解説記事も書くかもしれない。