神経科学は脳をどこまで理解したか
2019年6月に、『計算論的神経科学』(田中宏和著)が発行されました。
「計算論的神経科学」とは、脳を研究する「神経科学」の一分野です。同書の第0章から引用します。
計算論的神経科学が目指すものは,(1)神経系での情報処理における普遍的な原理を見出し,(2)その計算原理を解くのに適切な表現とアルゴリズムを定式化し,(3)その表現とアルゴリズムがどのように神経活動や神経回路として実装されているかを解明することで,「脳を理解する」ことである. (『計算論的神経科学』第0章)
脳の細胞を観察したり、その生理現象を調べたりするだけでなく、コンピュータの動作をアルゴリズムとして理解するかのごとく、高度なレベルで脳を理解しよう。そんな野心的な研究分野なのです。著者の田中宏和先生の研究室紹介の動画でも、わかりやすく解説されています。
この「計算論的神経科学」が、ここ数年注目を集めています。背景としては、
・ 脳の機能を知るための理論的アプローチの全体像を知りたい
・ 神経活動や行動データの背後にある脳の情報処理メカニズムを知りたい
・ 人の身体・認知機能の回復・増強に向けた、計測・制御の方法論を知りたい
・ ヒトや動物の神経系の制御機構を参考とし、ロボットの設計などへ応用したい
・ 脳のアーキテクチャや情報処理機構を参考とし、脳に学んだ人工知能を実現したい
といったさまざまな動機がありそうです。
では、そもそも脳はどこまで明らかになったのでしょうか。『計算論的神経科学』の第0章では、物理学と比較した際の、神経科学の現在地点を考察しています。同書より抜粋してご紹介します。
神経科学は脳をどこまで理解したか:物理学との対比
著:田中宏和
神経科学で脳をどのように理解していけばよいかを考えるうえで,より古くから成功を収めてきた科学との比較は有用である.ここでは,物理学との対比で考えてみよう.
観測から法則へ,そして法則から原理へ
どの科学分野でもまずは実験事実の観測から始まる.力学の歴史を例にとれば,ティコ・ブラーエの観測データの蓄積,ケプラーによる天体運動の法則の発見,そしてニュートンによる重力の逆二乗則の発見と力学の定式化へと進んだ.このように科学は,
(1)実験と観測,
(2)法則(規則性)の発見,
(3)一般原理
の順で発展する.デンマークのティコ・ブラーエ(Tycho Brahe, 1546-1601)は望遠鏡の発明以前に四分儀なる測量機器を用い,彗星や超新星を発見した.これは自然の素直な観測の段階と言える.観測の次に来るのは,その観測のなかに潜む規則性を見出す段階である.ティコの遺した膨大な天体運動のデータをもとに,弟子のケプラー(Johannes Kepler, 1571-1630)は有名な惑星運動の三法則(楕円運動の法則,面積速度一定の法則,調和の法則)を見出した.ケプラーがこれらの法則性を見出すことができたのは,古代ギリシャ以来暗黙に仮定されてきた,天体運動は完全な円運動であるという思い込みから踏み出して,実は楕円運動であることに気づいたからである.この法則により,地動説は天動説に対する優位性を確立することができた.ケプラーにとって,そして我々にとって幸運だったのは,空間が三次元だったということである.もし空間が二次元であれば重力は強すぎて地球は太陽に衝突してしまうし,逆に空間が四次元以上であれば重力は弱すぎて地球は太陽の重力に束縛されず無限遠方に飛び立ってしまうだろう.空間が三次元であることで安定な閉軌道をなすというのはベルトランドの定理の結果であり,地球が太陽の周りを何十億年も安定して回り続けることで,知的生命体が進化することができたのである.もし空間が三次元でなければ,天体運動に規則性を見出すのは難しいだろうし,そもそも生命が進化したかどうかもわからない.
ここまではデータから得られた規則性であり,天体運動以外の運動は考慮されていない.そしてクライマックスは,天体運動の法則からより一般的な力学の原理を導くことである.ケプラーが確立した地動説から,ニュートン(Isaac Newton, 1642-1726)は物体間の距離の逆二乗に比例する万有引力の法則を提案し,これもニュートンの発見である運動の法則と組み合わせて,ケプラーの三法則を説明することができた.ニュートンが天才たる所以は,天体運動から産まれた彼の力学が,天体運動を超えて万物の運動を記述する普遍的なものであったことである.優れた理論は,もともとその理論が説明すべき適用範囲を超えた普遍性をもつものである.
ミクロの理解とマクロの理解
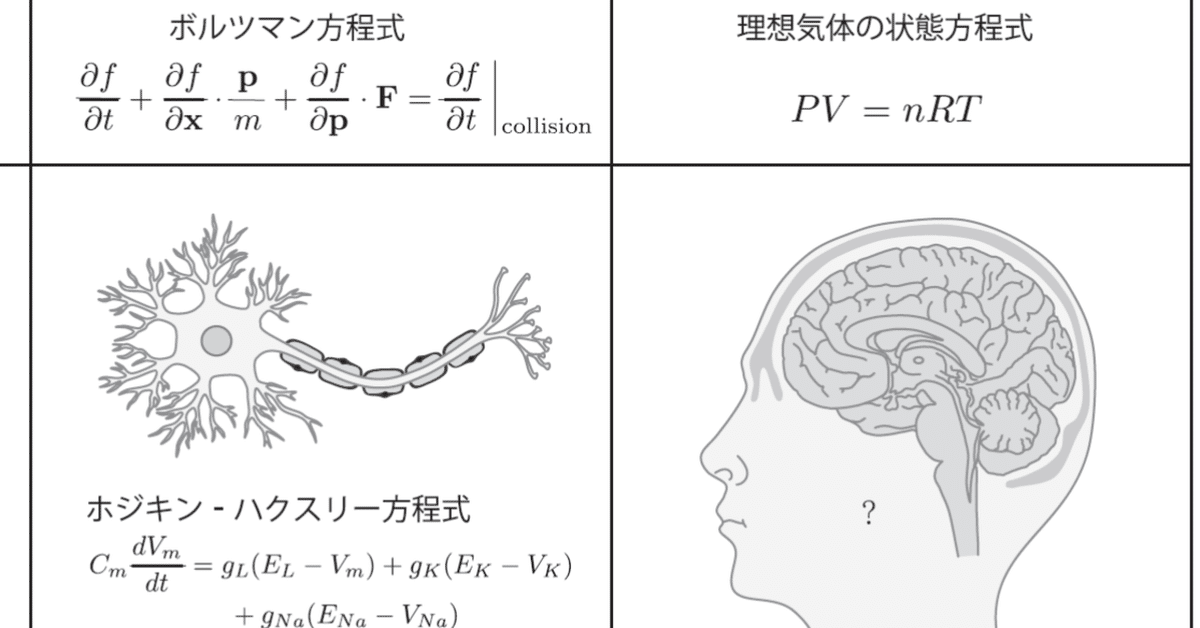
ある系を理解する方法は一つではなく,少なくともミクロ的観点とマクロ的観点からの理解がありうる.物理学で言えば,物質に対して分子論的な記述(ミクロな記述)と熱力学的な記述(マクロな記述)が可能であり,ミクロとマクロを繋げる理論として統計力学がある.物理学は経験科学であるから,単純で扱いやすく,かつ物理の本質を豊かに含む系を調べることが有益である.熱力学や統計力学では,そうしたモデル系として理想気体がよく取り上げられる.理想気体は,熱機関の理論的な効率を求めるためのカルノーサイクルの解析などに用いられてきた.理想気体を構成するすべての気体分子の運動と衝突を記述すれば,理想気体の振る舞いを捉えることができる.これはミクロな記述であり分子運動学と呼ばれる.一方で,気圧,体積,温度といったマクロな観測量を用い,それらのあいだに成り立つ熱力学的な状態方程式で記述することもできる.
ミクロ的記述とマクロ的記述は,どちらも同じ物理現象を記述する以上,同じ答えを出すはずである.一方,現象の理解という観点では,熱力学的な(マクロな)記述が優れている.熱力学は,分子の大きさや分子間の相互作用などといったミクロな詳細を知ることなく,気体の体積・圧力・温度といったマクロに観測可能な量を用いて,気体の振る舞いを記述できる.また熱力学では,たとえば気体に熱や仕事を与えたり,ある一つのマクロな変数を変化させたりしたときに,気体がどのような平衡状態に移行するかを記述できる.実際,量子力学の発見により,ミクロなレベルでの物質の理解が革命的変更を受けた後も,熱力学はまったく変更の必要がなかったのである.
もちろん,ミクロな記述において,膨大な数(アボガドロ数オーダー)の分子の運動を数値計算で解けば,熱力学と同じ答えが計算できるだろう.しかし,計算できることと理解できることは必ずしも同じでない.ある分子運動に摂動を与えた際の系の変化を予測するためには,ミクロなアプローチでは初期条件を変えた数値計算を繰り返す必要がある.しかしこれは計算機による現象の再現であり,それがうまくいったからといって,人間が理解できたとは言えない.理解したと言えるためには,「摂動を与えた際の系の応答が予言できること」だけでなく,「系の物理的振る舞いにとって本質的な変数を見出すこと」が必要である.物理現象をミクロな法則から説明できるという還元主義の立場もありうるかもしれないが,理解という観点ではマクロな法則のほうが優れているのである.
神経科学で足りないところはどこか?
物理学と比較した際に,神経科学の理論的アプローチで不足しているのは,理論の普遍性と予言能力である.大脳皮質・小脳・大脳基底核それぞれで確立した計算論モデルが提案されている一方,それらの理論が説明すべき守備範囲を超えた他の現象を説明する普遍性に欠けている.大脳皮質の計算モデルに限っても,感覚処理や運動制御の計算論モデルは多数存在するが,それらを俯瞰するような観点に欠けているのが現状である.この批判はもちろん筆者自身の研究にも当てはまる.何をどう研究すれば,「脳がわかった」という実感が得られるのだろうか.筆者自身,決定的な回答は持ち合わせていない.
本書〔『計算論的神経科学』〕で提示するのは,あくまで一つの可能なアプローチである.どの教科書にも同じような筋書きで同じような公式が書いてある物理学の教科書とは違い,神経科学の教科書は視点も内容もさまざまである.これは「脳を理解する」ことの意味が研究者一人一人で異なることを反映しているのだろう.「脳を理解する」とは何か,そのためにはどのような研究をすべきか,自分なりの考えをもつべきである.
物理学では19 世紀半ばにマクロ的視点の熱力学が確立し,その後20世紀初頭にかけてミクロ的視点の統計力学が発展した(図)†.
†言うまでもなく,統計力学と熱力学の関係はここに書いたほど単純ではない.田崎晴明『熱力学』(2000年,培風館)を参照のこと.
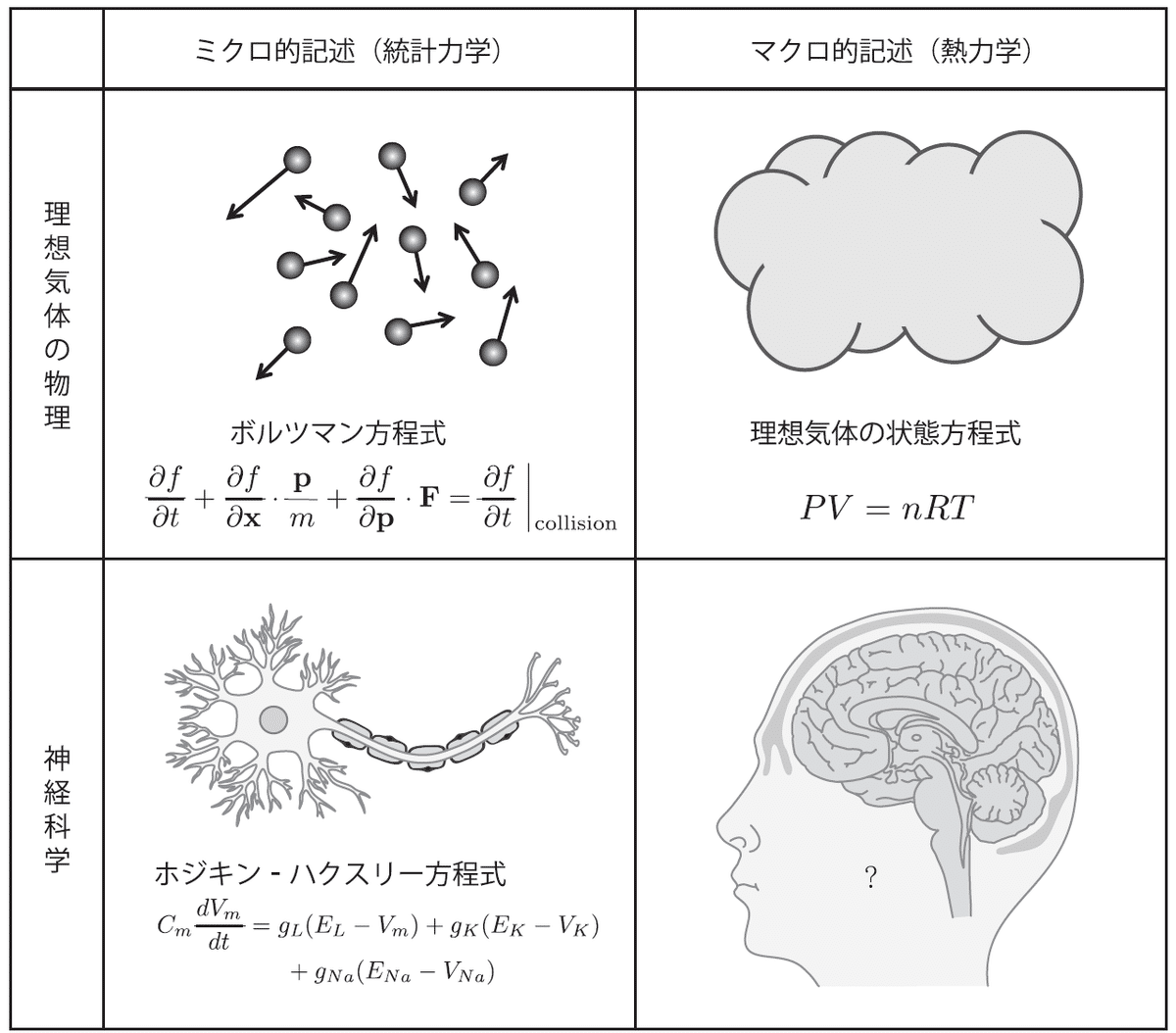
図:物理学(特に分子運動論)と神経科学におけるミクロ的記述とマクロ的記述.
幸運だったのは,多数の均一な気体分子が希薄に相互作用する系では,大数の法則や中心極限定理といった漸近法則が成り立ち,ミクロな分子の力学的性質の詳細がマクロな物理に効かないことである.そのため,ミクロの詳細がマクロの系には残らず,マクロな系の振る舞いが普遍性をもつ.もしミクロな詳細がマクロの系を大きく作用するような世界に住んでいたとすると,気体分子の種類に依存してマクロな性質が変わることになり,熱力学は普遍性をもたなかったであろう.自然は人間に理解できるような法則を用意してくれていたのである.
興味深い対比として神経科学では,まず神経興奮現象やホジキン-ハクスリー方程式といったミクロ的な視点での単一神経細胞に関する理解が進んだ.しかし,一つの気体分子の特定の運動が気体全体の振る舞いに影響を与えないのと同じように,一つの神経細胞の特定の発火が神経系全体に影響を与えないであろう.神経系全体にとって何が本質的な変数なのか,そしてどのような計算を行っているのかというマクロ的な視点に関して理解が進んでいないのが現状である.ラゼブニックのラジオの例で見たように,還元的なアプローチでは,特定の神経伝達物質や遺伝子などといったよりミクロで詳細なメカニズムの研究に進むことが多い.しかし不幸なことに,神経細胞の間の多種多様な相互作用のもとでは一般論として漸近法則が成り立たず,物理学のようにミクロの法則からマクロの法則を導くのが難しいのである.したがって数値的手法に頼るほかなく,たとえばヒューマン・ブレイン・プロジェクト(Human Brain Project)では,現在知られている解剖学的構造や神経細胞の形状や生理学的性質をすべて考慮に入れたヒト全脳神経系のシミュレーションを目指している(Markram, 2012).この種のシミュレーションは計算機の能力が向上した今日だからこそ可能になりつつあるものである.しかし,詳細なシミュレーションは脳の理解に繋がるだろうか.それは単なる計算機上の現象の再現にすぎないのではないだろうか.先ほどの気体分子運動論におけるアボガドロ数程度の分子運動のシミュレーションと同様に,脳の理解にはさほど役に立たないのではないだろうか(田中宏和,2009).本書では,全脳シミュレーションなどのアプローチとは異なる,神経科学のマクロ的記述を目指す理論的試みについて見ていきたい.
・ Markram, H. (2012). The human brain project. Scientific American, 306(6), 50-55.
・ 田中宏和(2009)「計算論的神経科学のすすめ:脳機能の理解に向けた最適化理論のアプローチ」,物性研究.
出典:『計算論的神経科学:脳の運動制御・感覚処理機構の理論的理解へ』(第0章、0.4節)
著者:田中宏和(たなか・ひろかず) 北陸先端科学技術大学院大学 准教授
***
『計算論的神経科学:脳の運動制御・感覚処理機構の理論的理解へ』は、運動制御を中心とした研究を数多く紹介しつつ、計算論的神経科学への入門に必要な数学の基礎もひも解いた一冊です。
【目次】
第0章 計算論的神経科学 ―なぜ脳科学に計算論が必要なのか
第1章 身体運動の基礎 ―キネマティクス・ダイナミクス・座標変換,それらの脳内表現
第2章 決定論的最適制御 ―運動の背後に潜む最適化の計算原理
第3章 状態空間モデル ―運動過程と観測過程のモデル化
第4章 最適推定 ―感覚入力からの外界再構成
第5章 確率論的最適制御 ―ノイズ下でも正確な運動を可能にする制御
第6章 強化学習 ―報酬に基づく運動学習
第7章 システム同定 ―運動適応過程のリバースエンジニアリング
第8章 次元縮約と成分分解 ―脳のなかの真の自由度
第9章 デコーディングとブレイン・コンピュータ・インターフェイス ―脳の情報表現を読み取る
第10章 小脳の計算論モデル

