
【算数】文章題のトリセツ 〜式よりイメージが大切!~
■本をたくさん読めば、文章題が解けるようになるのか?
「うちの子、文章題が苦手なんです。どうしたらいいでしょうか?」
小学生のお母さんと面談すると、かなり高い確率で出てくる相談事が「文章題を得意にするためにはどうしたらいいか」というものです。
この質問に対しての指導者は、学校・塾に関わらず、おそらく
「本をたくさん読んで読解力をつけましょう」
と答えることが多いと思います。
だけど、これは的外れな回答です。このアドバイスで文章題が得意になったという話は聞いたことがありません。一見説得力があるような感じがするので、保護者の方が納得してくれることが多い。ということで、指導者はつい口にしてしまいがちです。
ということで、かつて塾業界駆け出しの頃は私もこのセリフをさんざん使わせていただきました。今となっては当時のお母様たちに懺悔するしかないという気持ちでいっぱいですが。。。(^^;)
■なぜ多くの子どもたちは文章題が苦手なのか?
こんなにも多くの子が、なぜ文章題を解くことを苦手とするのでしょうか?
それは文章題を解くときの手順に問題があるからです。ふつう、小学生は文章題を次のように解くように指導されることが多いようです。
まず式を考えて、その式を計算して、答を出す。
実はこの方法、ものすごく難度の高い方法です。
そのことを実感していただける文章題があります。次の文章を読んで、まず式を立てて、答を出してみてください(これはうちの塾のオリジナルの小学生用文章題です)。
僕、アリのハッピー。
我が家の初詣は、毎年、近くのアナゴ神社と決まっている。
なかでも楽しみなのは、おみくじとお賽銭。
お賽銭は、十分ご縁がありますように、と毎年15円入れているんだよ。
ところで、アナゴ神社の階段は、全部で300段あるんだけど、
朝の7時半に登り始めて、40分かかって126段登ったところで、
もう息が切れちゃって・・・。ここで、10分間の休憩だ。
それから、残りの石段を1分間で3段ずつ登ったんだ。
さて、僕たちは何時何分に着いたのだろう。
いかがでしたか。
大人でも結構苦労されたか、もしくはややこしくて途中で断念された方もいらっしゃるかもしれません。ちなみに式は次のようになります(他にも方法はありますが一例として)。
300-126=174(ひき算)
174÷3=58(わり算)
40+10+58=108(たし算)
7時30分+108分=7時138分=9時18分(時間の計算)
答 (午前)9時18分
以上、4つの式を立てて、9時18分という正解を得ることができます。
■習っていなくても文章題を解くことができる
おそらく上記の文章題を解かれるときに、ちょっとした図を描かれた方は苦労することなく割とすんなりと式が出たのではないかと思います。
そうなのです。難しめの文章題に対しては、式を立てる前に図や絵を描いて考えることが大切なのです。
次の答案は、小2の塾生Sちゃんが上記の文章題を解いたときの答案用紙です(解いたのが12月末ですから、あと数ヶ月で3年生になるぐらいの時です)。

え、小2で?と思われた方もいらっしゃると思います。だけど、絵や図を駆使すれば、学校で習っていない内容の文章題でも意外と解けるものなのです。
この答案をよく観察すると、この文章題を解いた過程における思考の流れがよくわかります。小2の子どもでもこのように複雑な文章題をなぜ解くことができたか、おわかりいただけるのではないかと思います。
それでは、この答案をじっくりと観察していきましょう。
アナゴ神社の階段は、全部で300段あり、126段登ったから、残りの階段は求めるために、右上に筆算しています。
300-126=174(段)
残りは174段です。まだ割り算を学校で習っていないので、地道に石段を描いています。図より、残りの石段を登るのに58分かかることが分かりました。それに、途中までかかった40分をくわえます。
58+40=98(分)
これで階段を登っている間の時間が出ました。次に98分に休憩の10分を足して、108分にするのかな?と思ったら、98分から30分引いちゃいました。
98-30=68
おそらくここで、彼女の頭の中で30分は7時半に与えられ8時に変えて、時計の計算をしやすくしたと思われます。ここで、8時からどれくらい時間がたったかを求めます。まだ休憩の時間を加えていなかったことを思い出したのでしょう。
68+10=78
で、8時を基準にして、これから78分経つと、描いた時計を使って、
9時18分という答を導き出しています。
以上、ざっくりと見ていきましたが、この思考の流れの中で一番の難関の場所はおわかりですね。
「残りの174段を1分間に3段ずつ登る」です。
ここで、大半の小3以下のお子さんはあきらめてしまいます。174÷3のような「3桁÷1桁」の式は小4にならないと習わないからです(もし仮に式を立てることができても計算できません)。
「こんな問題、まだ習っていないからできるはずないじゃないか」と言って、多くの子は考えることを完璧に放棄してしまうことでしょう。
だけど、絵を描いて考える方法を知っている子は、習っているかどうかは関係ありません。とことん粘ることができます。ひたすら黙々と自分の力で考え続けるだけです。
わからないとぼやくより前に、とりあえず174段の石段を描けばいいだけの話です。
1分で3段、2分で6段、3分で9段・・・58分で174段というふうに数えていくわけです。
アリのハッピーと一緒に、登りながら。。。
一段
一段
一段
一段
一段
・・・
苦労しながら、やっと頂上の神社にたどり着きます。
そこで初めてわかります。
174段登るためには、58分もかかってしまうことを。
アリさんが石段を登るのが大変だと言うことを。
■複雑な文章題に隠れているたくさんの宝物!
ここで、多くの方はこんな面倒なことに時間をかけなくても、174÷3の式を立てて答を素早く出した方が効率がいいじゃないかと思われることでしょう。
常識的に考えれば、174÷3で簡単に答を出す方がレベルが高いし、短時間で効率よくたくさん問題が解けるから優れているということになります。
一方、絵を描いて楽しみながらだと、一題解くのがやっとです。たくさんの問題は解けません。効率性からいけば、最悪です。
だ・け・ど、正しい苦労は神様からのご褒美をたくさんもらえることになります。
お宝をどんどんゲットできるのです。特に複雑な文章題には隠れた宝物がたくさんあるからなのです。
その宝物を見つけなくても、答を出すことはできます。だけど、せっかくの宝物をみすみす見逃すなんてもったいないと思いませんか。
絵を描けば、宝物のありかが見えてきます。
では、お宝探しに出かけるとしましょう!
最初すぐに分かることは、石段を一段一段積み上げて描いていきますから、たし算を強烈に意識することになります。
『たし算』のお宝、ゲット!
それから、ここには描かれてはいませんが、頭の中で300段を描いて、
126段登った場面を想像して、300-126=174 をイメージしたわけです。
『ひき算』のお宝、ゲット!
右上に時計の絵を描いて、時間の計算をしていますね。
『時計算』のお宝、ゲット!
174段の石段を描き、その中に3段の固まりが何段あるかを意識しますね。
『わり算』のお宝、ゲット!
174÷3という式を意識していないかもしれませんが、まだ学校で習っていない『わり算』の原理をここでしっかりと学ぶことができるのです。
『わり算』の答を出すことのできる小学生はたくさんいますが、実はこの『わり算』を本当に理解して中学生に上がっている小学生は、私の主観ですが、全体の2割から3割ぐらいのような気がします。『わり算』は本当にむずかしい単元なのです。
ここで絵をよくご覧ください。60段までは根気よく「3段ずつで1分」とずっと描いていますが、ちょっとめんどうになったのでしょうね。60段以上では「30段で10分」ずつと、3段を10個集めて、30段にしています。
これを式で表すと、
3×10=30
『かけ算』のお宝ゲット!
では、そろそろ、より次元の高いお宝へとご案内です。まだ学校で習っていない単元のお宝が実はたくさん埋まっています。お気づきになっている方も多くいらっしゃると思いますが、実はこの問題。小6で習う『速さ』の問題なのです。
問題文の中に「残りの石段を1分間で3段ずつ登ったんだ。」という部分があります。ここが『速さ』問題のポイントになります。
『速さ』の問題において
「1分間に3m」が「分速3m」に置き換えることができるように、
「1分間に3段」は「分速3段」という速さの表現に置き換えることが可能です。
ですから、さきほど無意識に獲得した割り算の原理のもとの174÷3の式は、速さの3公式のうちの「時間=距離÷速さ」の公式に数値をあてはめた式と同じなのです。
174(段)÷3(段/分)=58(分)
図を描いて解くことにより、「速さ」の問題を自分の納得できる範囲で、感覚的に学ぶことができとういうことになります。
『速さ』というお宝、ゲットですね。
そうなのです。まだ習っていない単元は、解き方を教わらなくても、前もって学習できるのです。これはいわゆる『先行学習』とはちがいます。解き方をだれかに教えてもらって暗記するのではありませんから。自ら試行錯誤することによって得られるものです。
まだまだ、お宝さがしは続きます。
同時に、『速さ』の問題がもたらす意味を、実に深~く学ばさせてくれます。
1分 … 3段
2分 … 6段
3分 … 9段
4分 … 12段
・・・
58分 … 174段
と並べると、もうおわかりですね。
「時間」が2倍になると、「石段の数」も2倍になっている。
「時間」が3倍になると、「石段の数」も3倍になっている。
・・・
「時間」が58倍になると、「石段の数」も58倍になっている。
「時間」と「石段の数」が『比例』の関係になっています。これは小6で習います。
『比例』のお宝、ゲット!
さらに、同じく小6で習う、
1:3=2:6=3:9=・・・=58:174
の『比』の関係も観察できます。またまたお宝です。
『比』のお宝、ゲット!
これらを見て、この関係を『比例』だとか『比』という用語を子どもに教えることは、ほとんど無意味です。
大切なことは、「『比例』や『比』の関係をじっくりと肌で感じていく」ということ。こうして『比例』や『比』の原理が深~く深~く無意識層という名の意識層に刻み込まれていくのです。
また、この絵を抽象化すると、次のような表になり、
時 間 1 2 3 … 58
石段の数 3 6 9 … 174
さらに、中学ではこの表が、次のようなxとyを使ったものに発展し、
x 1 2 3 … 58
y 3 6 9 … 174
この表を、さらにもっと抽象度を高めたものがグラフです。
そのグラフの式が、一般式と呼ばれる y=ax です。(比例の関係においては、aは比例定数と呼ばれますが、その本質は、一次関数のグラフにおける「傾き」、または「xが1増加したときのyの増加量」つまり「変化の割合」ということになります)
中学生にとって、y=axのaを本当に感覚的に理解している子はごくごくわずかで、ほとんどの中学生は、y=axの式にxとyの数値を代入して、わけもわからずaを出しているだけというレベルです(これでも、テストの点数は取れるのですが…)。
絵を描けば、中学生がほとんど理解できていない「変化の割合」も言葉を通さずして、深層意識の中に刻みつけていくことになるのです。
「y=ax」の理解の鍵は、このaの理解にあります。
xが1増えると、yは3増える。
またxが1増えると、yは3増える。
またxが1増えると、yは3増える。
・・・
時間が1分経つと、石段を3段のぼっている。
また時間が1分経つと、石段を3段のぼっている。
また時間が1分経つと、石段を3段のぼっている。
・・・
つまり、アリのハッピーになりきって、アナゴ神社という一次関数の石段(グラフ)を、よっこらしょ、よっこらしょとのぼる。
この疑似体験が、そのまま中学で習う関数のグラフのイメージに結びついていきます(これこそが体験学習の原点です。具象世界と抽象世界を行ったり来たりすることが生きた知識となりうるのです)。
神社の石段の傾きのイメージは、そのままy=axのグラフの傾きにオーバーラップされていく。
この緻密な作業の繰り返しで、一般に「比例定数」と呼ばれる、この得体のしれない「a」の感覚が、無意識的に、だけどしっかりと育っていくのです。
『一次関数における「傾き」と「変化の割合」』のお宝、ゲット!
■習うまえにすでにわかっている世界
ここで、このあたりの話がよく理解されにくいかもしれませんので、『バカの壁』で有名な養老孟司先生のお力を借りることにします。
脳の専門家でいらっしゃる養老先生が、子ども向けにお書きになった本『バカなおとなにならない脳』の中で、このことに関連して述べていらっしゃいます。やや長くなりますが引用します。
繰り返しで、人は学ぶ
で、脳の活動は、ずっと一生その繰り返しなんです。だから根本的には脳は、このくり返しでつくられます。しかも、毎回くり返しているようでいて、少しずつらせん状に上っていくみたいに、そのくり返しから、いつの間にか脳は変わらない規則を学習していくんです。一回ごとのくり返しをすべておぼえていたら、頭は破裂しちゃいますから、そういうことは脳は関知しないんです。脳がやるのは、くり返しやってもいつも変わらない、ということの規則を、いつの間にか学習しているということなんです。
この学習が積み重なると、どうなるか。
たとえば、比例するふたつの三角形。ひとつは遠くにあって、ひとつが近くにあるとするでしょ。それをしょっちゅう、いろんなところから見ていると、最終的に脳ミソが何をおぼえこむかというと、比例関係なんです。そんなふうに、脳は、あっちからもこっちからも、いろんな距離から見ているあいだに、変わらないこと、変わらない性質だけを、おぼえていくんです。
で、算数で比例を習うと、ふつうはキミたち、外側に「比例」という規則があって、その、外側にある規則を自分が学んでいるんだ、なんて思ってるでしょう。
ぼくが言いたいのは、キミの頭の中に、くり返し学んだすえにすでにわかっている「比例関係」がじつは最初からあるんだっていうことです。むずかしく言うと、外部的に外側から説明してもらうと、頭の中にあるから、わかる、ということ。それが脳の働きというものなんです。ふつう考えるのと、ちょうど逆でしょ。
それと同じことで、キミたちは学校で、外からいろいろ教えられるもんだと思っているでしょう?でも、そうじゃない。わかるというのは、もともと自分の中にわかるだけのものが、ループのくり返しによりでき上がっていて、それを外から説明されるから、わかるんだ。
養老先生が説明されているように、自分の頭の中にすでに「わかるものだけのもの」があるときに初めて理解が成立するのです(だから、幼児期はたくさん遊んで「目に見えない学力」を鍛える絶好の時期。机についてプリントをやっている暇はないのです。「目に見える学力」は「目に見えない学力」に支えられているわけですから)。
分からない子にいくら説明してもなかなかピンときてもらえないのはそのためなのです(学校や塾の先生はそれこそいやというほど体験されていますから、ここのところは文字通りピンと来られると思います。これもループのくりかえしのおかげですね)。
というわけで、幼児期の様々な遊びの体験が実は学習に役立っているんだということがわかります。いわゆる早期教育はその機会をどんどん失う可能性があるということも同時に意味しています。
あ、そうそう、そういえば、言い忘れていました。
お宝、まだありました。
『ドッカイリョク』というお宝。
これは算数の文章題なのですが、実は国語の読解力もつけてくれるのです。「文章を読んで、絵に描いて表す」ということは、文を読むときにいつもイメージすることを意識しながら読むことにつながるのです。
■文章題を解く目的は、答を出すことではない
こんなにじっくり解いていたら、テストで良い点数とれるかどうか心配だ、という声が聞こえてきそうです。
そう。おっしゃる通りです。
確かに目の前のテスト対策で文章題を解くのでしたら、一般的な方法が有効でしょう。だけど、文章題を解くことを通して、お子さんの地頭を鍛えたいのであれば、「急がば回れ!」です。絵を描き、じっくりと考える解き方をお勧めします(複雑な文章題をじっくりと絵(図)を描いて解けるようになれば、学校のテストの文章題もかんたんな図を描いて、または頭の中で軽くイメージして解けるようになることも多いですが、そのことは私にとってはあまり関心がありませんので、これ以上触れないでおきます)。
この「地頭を鍛える世界」においては、答なんて、まちがってもいいのです。大切なのは、自分だけのお宝を見つけること!これこそのみが、この文章題を解く最大の目的なのです。
イメージとしてのお宝をがっぽがっぽ獲得しちゃいましょ。まちがってもいいのだから、子どもたちにとっても気楽に取り組めますね。プレッシャーなしのリラックスした状態が大切です(リラックスした状態が一番力が出せるというのはいろんな方がおっしゃっていますね)。
ともあれ1題をじっくりと解くだけで、いろいろなお宝をゲットできることがおわかりいただけたと思います。1週間に1題で十分です。じっくりと絵を描きながらですので、結構楽しめます。だけど、楽しいからといって、毎日解かせるのはよくないですよ。飽きてしまいますから。
いくらビフテキとトリの唐揚げが大好物だからといって、毎日食べさせられたら、モー、ケッコーと言いたくなりますよね。
さあ、子どもたち!
君たちも、アリのハッピーと一緒に、
石段を一段一段登ってみないかい。
汗をかきかき苦労して登り切った後には、
おいしいおやつとジュースが待ってるよ!
PS
この記事の中の文章題は私自身が塾生用にこれまで作成してきたもので、全くのオリジナルです。次の記事の中で『絵解き「お話」文章題』(520題、PDFファイル)を販売(1000円)しております。
※ 無料体験版(30題、PDFファイル)で中身をご検討いただけます。↓
※次の動画はこの記事の動画バージョンです。特に「アリのハッピーの文章題」について詳しく解説しています。
最後に、他の塾生の答案を他にも載せておきますので、参考までにご覧になってください。
<小4の生徒さんの作品>
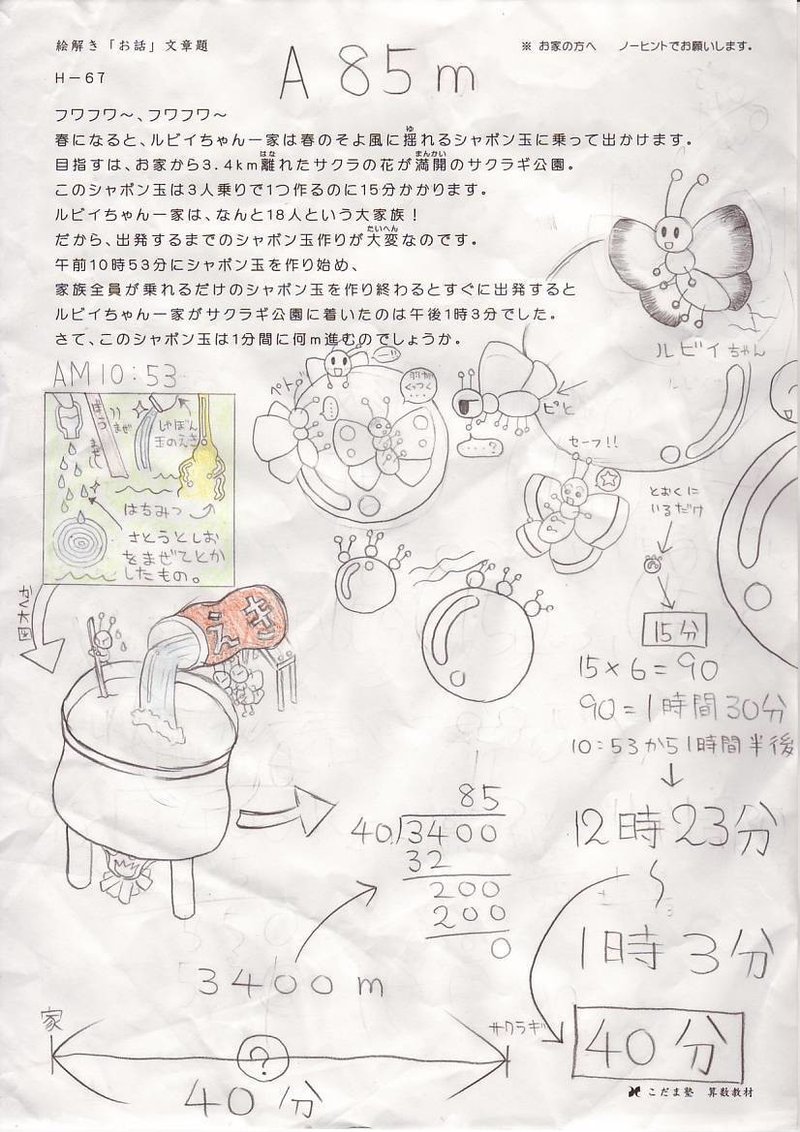
<小3の生徒さんの作品>
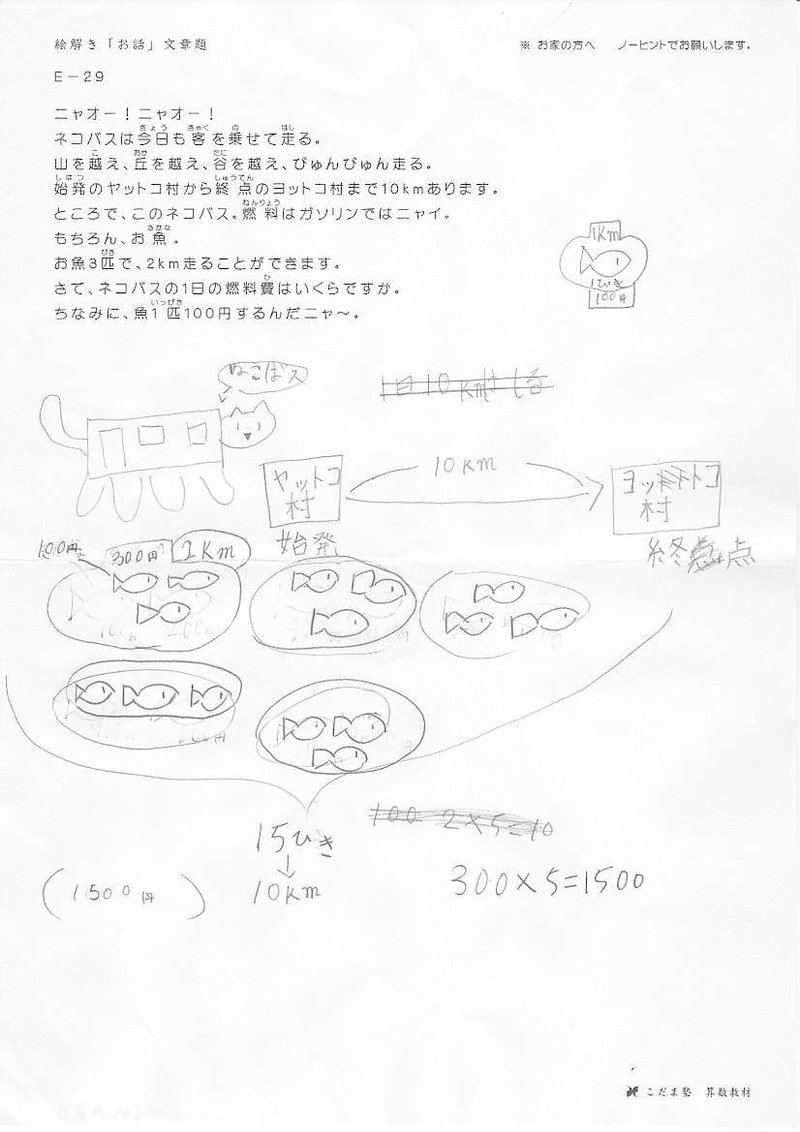
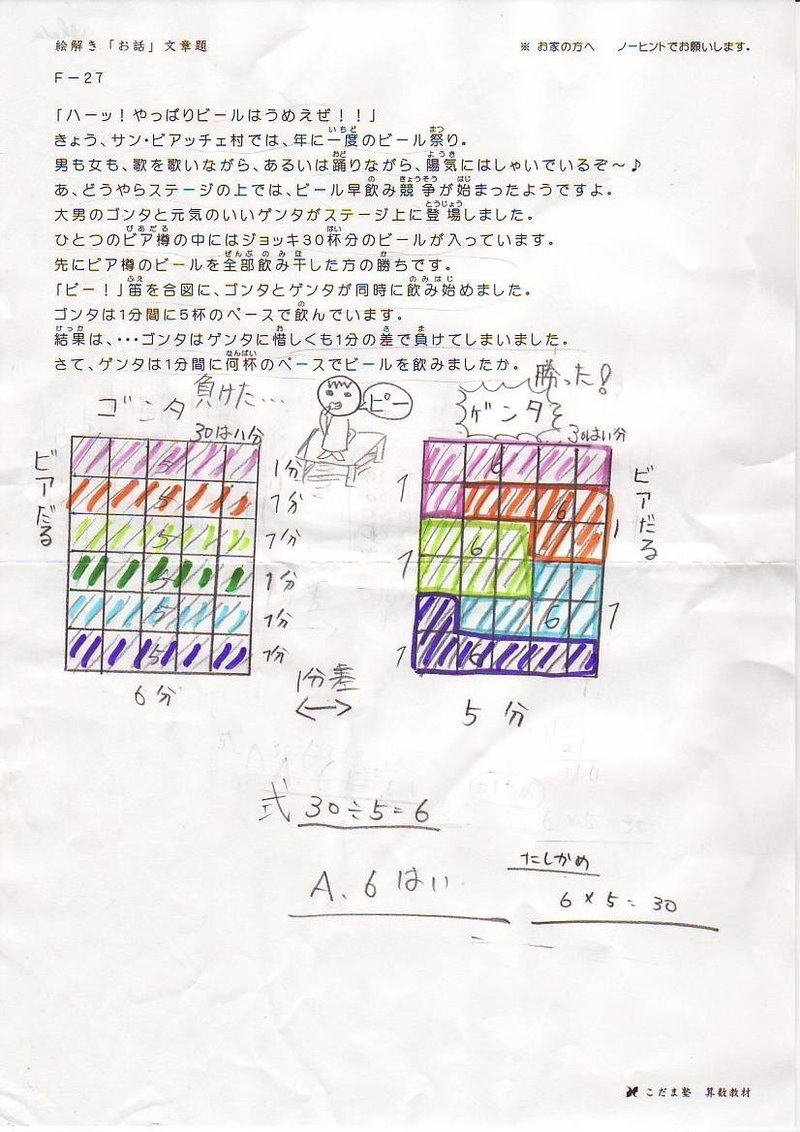
この記事が気に入ったらサポートをしてみませんか?
