
流体力学 カルマン渦列(その1)
皆様おはこんばんちは。
最近,流体力学を再度学び直してみようと思い,記事にしています。
第44回目は,「カルマン渦列」について紹介していきます。なお,カルマン渦列は連載企画とし,予定ではその3まで(但し,カルマン渦列(その3)は,名称が変わる予定)記事にする予定です。
(1)カルマンについて
では,「カルマン」について,解説していきます。カルマンとは,人物の名前です。
まず,人物から紹介します。上記の渦を見つけた方は,「セオドア・フォン・カルマン(1881-1963)」というハンガリーの航空工学者です。さらにユダヤ人でもあります。
彼は,ライト兄弟が世界初の有人動力飛行を達成した後に航空(空気)力学の業界で大きく活躍します。大学や航空研究所での勤務を経て,空軍という新たな軍事力を備えるための研究にも従事していたそうです。また,カルマンは日本の川西航空機で風洞実験を行うための風洞設計もしていたそうで,日本にも縁がある方だそうです。
次に,カルマン渦列の現象についてです。カルマン自身は,「カルマン渦列の安定(1911)」の著書でカルマン渦の発見とその理論について証明をしたそうです。発見までの経緯は,渦を見つけるための実験をしていた訳ではなく,円柱境界層の剥離の実験で円柱の振動対策に苦心しているときに偶然円柱後流に発生していた渦を発見したそうです。
このように素晴らしい功績を残されているカルマン先生ですが,次項では,カルマン渦列の理論に触れていこうと思います。
(2)カルマン渦列について(準備編)
ここでは,カルマン渦列の理論について触れていきます。カルマン渦は,静止している液体中に円柱のような物体を動かすとき,物体の背後に2列になって渦が発生することを指し,渦列となります。
図1に示すようにカルマン渦列の特徴は,一方の列の渦はすべて同じ方向に回転しているのに対し,他の列はすべて反対方向に回転していることです。

図1 カルマン渦列のモデル
図に示す通り,それぞれの列における渦の間隔a,2列の間隔b,上の列の循環Γ,下の列の循環-Γ,y軸に最も近い渦のx座標の距離x0と置きます。また,2つの渦列に中間にx,y軸をとり,特にy軸上に上の列の渦の1つを通過するような直交座標を考えます。
今回取り扱うのは,渦が一直線上にいくつも存在する状況です。これを渦の層と呼ぶことにして,図1のような状態を示します。このときのカルマン渦列全体のx,y軸方向の速度成分はそれぞれ式(1)のように表せます。

式(1)から分かるようにかなり煩雑な式で構成されています。では,この速度成分を証明するためには,カルマン渦列の複素ポテンシャルから共役複素速度を算出することで求められます。
(3)複素ポテンシャルについて
それでは,カルマン渦列の複素ポテンシャルについて見ていきましょう。この複素ポテンシャルは,以前の記事で紹介した渦列の複素ポテンシャルと同一となります。
但し,直交座標から渦までの距離が異なりますので,その距離に合わせて書き換えると,式(2)のように表せます。

よって,この式(2)を用いて,左右に渦列があることを考えると,式(3)のように書き換えられます。
![]()
では,複素ポテンシャルの準備ができたところで,次項では共役複素速度を算出してみましょう。
(4)共役複素速度について
では,前項でカルマン渦列の複素ポテンシャルが準備できたので,式(3)を使って共役複素速度を算出すると,式(4)のように表せます。

式(4)は非常に煩雑な式ですが,このままでは次に進めません。そこで,以前の記事でも紹介している渦列の共役複素速度を考えます。但し,原点に渦が存在し,その隣に別の渦があると仮定しています。その仮定をした共役複素速度を式(5)のように表せます。
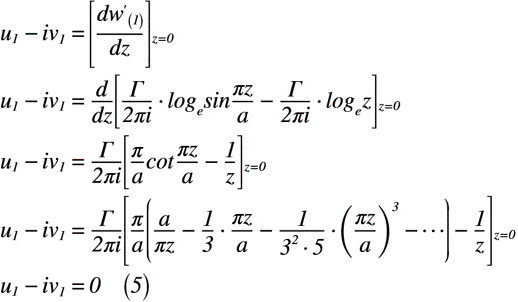
式(5)の結果を式(4)へ代入すると,式(6)のように表せます。

式(6)を見ると,式(4)と比べて,かなり簡易な形になり,計算が出来そうな雰囲気が出てきました。ここで,さらに式変形を進めるためには,複素関数の三角関数を考える必要があります。そのため,三角関数の式変形を進めていくと,式(7)と式(8)が得られます。


式(7)と式(8)を式(6)へ代入すると,式(9)のように表せます。

式(9)を見ると,三角関数の括弧内に複素数が含まれていることが分かります。そのため,これ以上の式変形を進めるには,複素関数の双曲線関数を考える必要があります。必要なものは,以下に示すような,式(10)および式(11)となります。


式(10)および式(11)を式(9)へ代入すると,式(12)のように表せます。

ここまで,何とか式変形を繰り返してきた式(12)を使って,カルマン渦列の共役複素速度である式(6)へ代入すると,式(13)のように表せます。

この結果から,式(13)を使ってx, y軸方向の速度成分u, vをそれぞれ示すと,式(14)のように表せます。

この式(14)が式(1)と同一となったため,カルマン渦列の速度成分を算出することができました。煩雑な式の理由は,複素関数の三角関数と双曲線関数の式変形と渦列の共役複素速度の仮定を使うことが主な理由だと思われます。
式(14)の結果から,カルマン渦列の速度成分に影響を及ぼす因子は,渦の間隔a,2列の間隔b,y軸に最も近い渦のx座標の距離x0の3つしか存在しないことも分かります。
(5)まとめ
今回の記事のまとめを以下に示します。
(1)カルマン渦は,一方の列の渦はすべて同じ方向に回転しているのに対し,他の列はすべて反対方向に回転している渦列のことである。
(2)カルマン渦列の複素ポテンシャルは,渦列のときと同様の式を用いる。
(3)共役複素速度は,渦列の共役複素速度がゼロになることを利用して算出する。
以上です。最後まで閲覧頂きありがとうございました。
次回は,「カルマン渦列(その2)」について,解説する予定です。
サポートをして頂けると大変助かります。何かの支援ができるかもと思われた人をは何卒よろしくお願いします!
