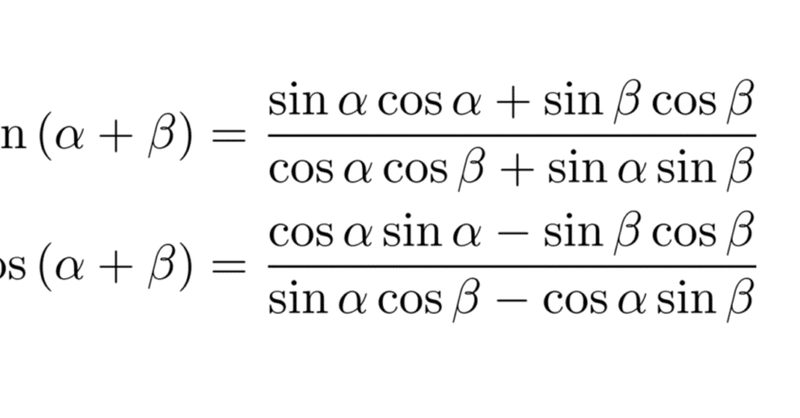
見たことのない加法定理

数学教室和(なごみ)講師の松中です。

和(なごみ)の講師は有志で常時いくつかの数学ゼミを定期的に開催しています。現在開講しているのは以下の4つです。
・ゲージ理論(今のところほとんどはリーマン幾何)
・微分幾何(ちょっと前までは素粒子物理をやっていた)
・多変量解析
・リーマン面

私は現在、ゲージ理論とリーマン面のゼミに参加しているのですが、リーマン面のゼミの中で今まで見たことのなかった三角関数の加法定理を発見したので、ご報告させていただきます。

加法定理

加法定理とは高校で学ぶ三角関数の公式です。

加法定理の覚え方はいろいろあるみたいですが、私は
・sinはsincos、cosはcoscos、後半はその逆
・α、βの順番はそのまま
・cosの方は符号が逆になる
と、断片的なルールで覚えました。

私は高校時代に覚えようと意識して覚えた公式はこれだけだと思います。他の公式は、形が単純だったり、意味を考えれば明らかだったり、という理由で使っているうちに自然に覚えられるものと、複雑すぎるから覚えるのをあきらめて定義や他の公式から導出すると決めたものに分けられます。

加法定理はそれなりに複雑な上、cos、sinの定義や他の公式から導出するには少し手間であるため意識的に覚えました。余談ですが、東京大学の入試問題には「加法定理を証明せよ」という問題が出たことがあります。東京大学を受ける方であれば加法定理は当たり前に使いこなしているはずですが、いざ証明しろと言われると難しいのかもしれませんね。

cosの別の定義

さて、リーマン面のゼミでは「リーマン面の理論」というテキストを読んでおり、第1章ではcosを高校とは異なる方法(代数的関数の積分の逆関数)で定義し、そのアナロジーで楕円関数を導入しています。本記事には関係はないのですが、こちらがこのテキストでのcosの定義です。

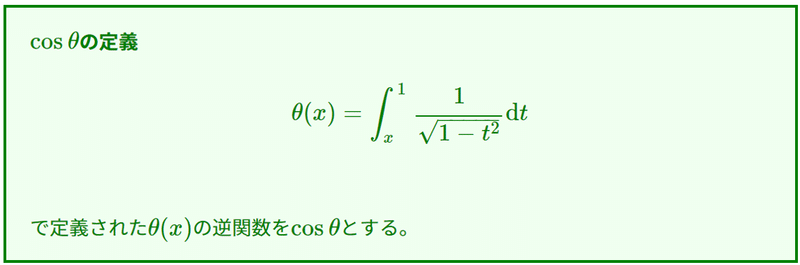
同じcosなのに、いろいろな定義があって面白いです。ちなみに私が大好きなcosの定義はこちらです。

円も、円らしき数式も出てこないこのシンプルな微分方程式で三角関数を定義できるとは驚きです。なんとこの定義をするとπの定義はこうしてもよいことになります。

π≡inf{θ>0|s(θ)=0}

通常πは直径と円周の長さの比で定義されるため「円周率」と呼ばれますが、それはπが持つたくさんの顔の1つに過ぎないのでしょう。

話がそれましたが、テキストではその後、楕円関数の加法定理を導くために、cosの加法定理の証明のアイディアを述べています。その方法も高校で一般に習う方法とは異なるもので、円周上の点の運動に注目しています。

元々のアイディアは高校数学+α(物理、微分方程式)なのですが、実際に行う計算自体は高校数学で簡単にできるものです。加法定理は高校時代からよく知っているので、詳細に立ち入らず飛ばすこともできたのですが、ゼミということもありせっかくだから計算してみました。

当たり前の加法定理が当たり前に出てくるだけ。軽い気持ちでほとんど機械的に計算を続けていたのですが、どうしてもよく知っている加法定理が出てきません。何度計算しても、です。そこで気づきました、これは今まで見たことのない加法定理なのだと、、、

続きはこちらから

見たことのない加法定理｜マスログ

<文/松中>

「数学教室和(なごみ)」では算数からリーマン予想まで、あなたの数学学習を全力サポートします。お問い合わせはこちらから。お問い合わせページへ