#数学
【複素解析】ゼータ正規化でsinが出るやつ
以前単純な場合でのゼータ正規化を求めた。
ここでは
$$
\prod_{n=-\infty}^{\infty} (n+a)=-2i\sin(\pi a)
$$
を求めていく。(参考文献:江口徹, 菅原裕二「共形場理論」)
ゼータ正規化ゼータ正規化は形式的には「総乗の中にゼータ関数を見出して置き換える」ことで行える。つまり
$$
\zeta(s)=\sum_{n=1}^{\infty} \
【複素解析】純虚数を引数に持つガンマ関数の2乗
有名なはずなのに意外とネット上では見なかったので(全然ありそう)。実数$${x}$$に対して
$$
|\Gamma (ix)|^{2}=\frac{\pi}{x \sinh{ \pi x}}
$$
のように双曲線関数が出るというもの。
使うもの相反公式
$$
\Gamma(z)\Gamma(1-z)=\frac{\pi }{\sin{\pi z}},\quad z\in \mathbb{C
【Fourier解析】デルタ関数を級数展開してみよう
この記事はDiracのデルタ関数を複素Fourier級数展開してみようというもの。意外とFourier変換に比べて出現頻度は低い……?と思ったときに限って出てくるので一応まとめておく(閉弦の扱いがさあ!一瞬迷ってさあ!)。
まず、複素Fourier級数展開は関数$${f(x)}$$が$${x\sim x+2\pi}$$で周期的としたとき
$$
f(x)=\sum_{n\in \mathbb{Z
【複素解析】自然数を全部かけたら√2π??
こんな公式がある。
$$
1\times 2\times 3\times \cdots = \sqrt{2\pi}
$$
は?
$$
\prod_{n=1}^{\infty} \frac{c}{n}=\sqrt{\frac{1}{2\pi c}}
$$
えぇ……
これらは$${\zeta}$$関数正規化を行うことで正当化される。もちろん、通常の意味では当然発散するし、意味のない式である。
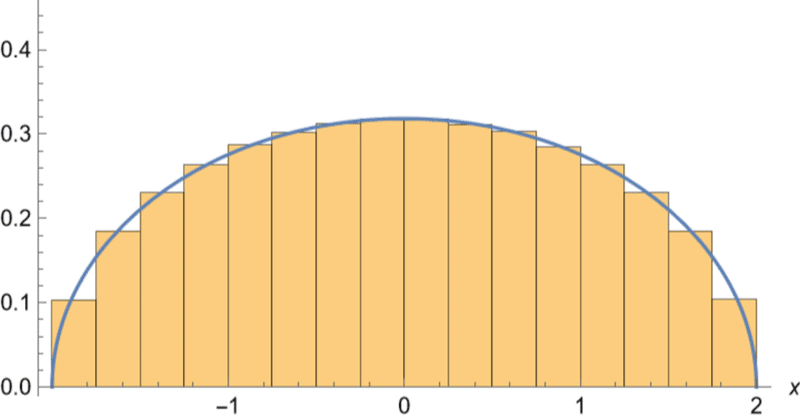
【ランダム行列】MathematicaでWigner半円則を見てみよう
タイトルの通り、この記事ではMathematicaを用いてWigner半円則を見る。ただ確認にすぎないが、意外と日本語の情報が少ないので記した。同様の話題で書かれた記事もすでにあるにはあったが、それは本来Wigner半円則と呼ばれるものではなかったというか、私がほしかった情報ではなかったので、改めて本稿で紹介したいと思う。
Wigner半円則これはランダム行列の理論で、ポテンシャルをGauss型
【微分幾何】多脚場を用いたときの測度との関係について
やること題名のつけかたに迷ったが、導きたい式は以下である。
$$
e^{1}\wedge e^{2} =\sqrt{g}d^{2}x
$$
簡単のため2次元で行っている。
ここで正規直交な1形式を$${e^{a}=e^{a}_{b}dx^{b}}$$と2脚場で表し、計量はEuclid化されているとする。つまり$${ \eta_{\mu\nu}=\delta_{\mu\nu} }$$である。なお