見出し画像

[デュエプレ ]レート1700は勝率◯◯%!!

くりりん

はじめに

こんにちは。くりりんです。
デュエプレ のランクマッチにおいて「レート1700」というのはトッププレーヤーであることを表す一つの称号となっており、これを目標としているプレイヤーも少なくありません。最近(2022年8月現在）ではレート1700台に乗るとその月のカップにおいて全プレイヤー中のトップ10近くに入ることになる[1,2]ため、これは紛れもなく強者の証といって差し支えないでしょう。

では、この「レート1700」を目指すためには具体的にどのくらい強くなればいいの？という事が気になってきますよね。
この記事ではその指標の一つとして「レート1700を維持するために必要な勝率」をいくつかの仮定のもとで計算してみました。
（瞬間的に上振れて1700に到達するだけであればこの限りではありません。）

獲得レートの計算式

まず一つ目の準備として、ランクマッチで1試合行った際のレートの変動について考えます。
デュエプレのランクマッチマスター帯のレートは定数$${K=16}$$のイロ・レーティングシステムという計算方法で決まっているようです[3]。

これによると一回の試合で変動するレートは自分と対戦相手とのレート差のみに依存し、
レート差を$${x=（相手のレート）-（自分のレート）}$$とした時
勝ったら$${+16\frac{1}{1+10^-\frac{x}{400}}}$$
負けたら$${-16\frac{1}{1+10^\frac{x}{400}}}$$
だけレートが変動します[4]。

また後ほども言及しますがデュエプレのランクマッチではレート差200
以内の相手とのみマッチングする[5]ようです。そこで、勝った時に獲得するレートを対戦相手とのレート差$${x=-200\sim 200}$$に対してプロットしてみました。

レート差と獲得できるレートの関係

また敗北時に失うレートはこれを左右反転させたようになります。

せっかくなので、一勝でもらえるレートの最大値と最小値を求めておきましょう。
$${x=200}$$で勝った時、つまり自分よりレートが200高い相手に勝った時獲得レートが最大になり、$${+16\frac{1}{1+10^-\frac{200}{400}}=+16\frac{\sqrt{10}}{\sqrt{10}+1} \approx 12.16}$$だけもらえます。
一方$${x=-200}$$で勝った時、つまり自分よりレートが200低い相手に勝った時獲得レートが最小で、$${+16\frac{1}{1+10^\frac{200}{400}}=+16\frac{1}{\sqrt{10}+1} \approx 3.84}$$だけもらえます

なおtwitterなどで検索してみると、1試合でレート$${\pm13}$$獲得した/失ったという旨のツイートが見受けられます[6]。（$${\pm14}$$以上は見つかりませんでした。）一見上記の計算と合わないように見えるかもしれませんがこれはおそらくゲーム内のレートの表示方法による問題だと考えられます。
例えば対戦前の自分のレートが1500.4だったとしましょう。小数点以下は（おそらく）四捨五入されて表示されているのでゲームの画面上では1500と表示されます。この時レート1700.4（レート差+200）の相手に勝ったとするとレートが+12.16されるため対戦後の自分のレートは1512.56となりこれが四捨五入され、画面上の表示は1513となり、表示の上では+13されたように見えるということなのでしょう。
同様の理由で、例えばレート1499.5（表示上1500)の状態でレートが200低い相手に勝った時、対戦後のレート1503.34（表示上1503)となって表示上+3しかされていないように見えることもある[7]と考えられます。
なので実際の獲得できる/失うレートは3.84~12.16だけど、表示上は3~13になるということなのでしょう。

マッチング相手のレートの分布

次に2つ目の準備として、マッチングする相手のレートの分布を考えてみます。

まず、マスター帯全体のレートの分布が中心1500,分散$${\sigma^2}$$の正規分布$${N(1500,\sigma^2)}$$に従っているとします。

中心1500の正規分布

この時、レートが微小な区間$${x\sim x+dx}$$の範囲にある人の割合は$${\frac{1}{\sqrt{2\pi \sigma^2}}e^-\frac{(x-1500)^2}{2\sigma^2}dx}$$で表されます。

分散は分布の広がり具合を表す量で、これは時間とともに大きく変動すると考えられるため、一旦$${\sigma^2}$$とおいたまま計算を進め、後半で詳しく考えることにします。

対戦相手のレートが単純にこの正規分布に従って確率的に決まるのであれば話は楽なのですが、先程述べたようにデュエプレではレート差$${\pm{200}}$$までの相手としかマッチしないため、実際はこのうち、自分とレート差$${\pm{200}}$$以内の人全員の中からランダムで選ばれるとします。例えば自分のレートが1600の時は下図のように
レートが1400~1800の人の中からランダムにマッチすると考えます。

マッチングの分布

なのでこの時、自分とのレート差$${x\sim x+dx(-200< x<200)}$$の相手とマッチングする確率は、対戦前の自分のレートを$${R}$$,自分とのレート差$${200}$$以内の人の全体に占める割合を$${N(=\int^{200}_{-200}\frac{1}{\sqrt{2\pi \sigma^2}}e^-\frac{(R+x-1500)^2}{2\sigma^2}dx)}$$として、$${\frac{\frac{1}{\sqrt{2\pi \sigma^2}}e^-\frac{(R+x-1500)^2}{2\sigma^2}dx}{N}}$$と表されます。

獲得できるレートの期待値と釣り合いの勝率

以上で求めたレート差$${x}$$の相手とマッチする確率とその試合後のレートの変動の値を使って、自分がレート1700($${R=1700}$$)にいて勝率が$${p}$$の時、1試合でのレートの変化量$${\Delta{R}}$$の期待値$${E[\Delta{R}]}$$を計算してみましょう。

期待値の定義に従って計算すると
$${E[\Delta{R}]=\int^{200}_{-200}[p\frac{16}{1+10^-\frac{x}{400}}-(1-p)\frac{16}{1+10^\frac{x}{400}}]\frac{\frac{1}{\sqrt{2\pi \sigma^2}}e^-\frac{(x+200)^2}{2\sigma^2}dx}{N}(期待値の定義）\\ \\=16\int^{200}_{-200}[p-\frac{1}{1+10^\frac{x}{400}}]\frac{\frac{1}{\sqrt{2\pi \sigma^2}}e^-\frac{(x+200)^2}{2\sigma^2}dx}{N}([   ]内を通分して整理）\\=16\int^{400}_{0}[p-\frac{1}{1+10^\frac{t-200}{400}}]\frac{\frac{1}{\sqrt{2\pi \sigma^2}}e^-\frac{t^2}{2\sigma^2}dt}{N}(t=x+200で置換)\\=\frac{16}{N}[p\int^{400}_{0}\frac{1}{\sqrt{2\pi \sigma^2}}e^-\frac{t^2}{2\sigma^2}dt-\int^{400}_{0}\frac{1}{\sqrt{2\pi \sigma^2}}\frac{1}{1+10^\frac{t-200}{400}}e^-\frac{t^2}{2\sigma^2}dt]}$$

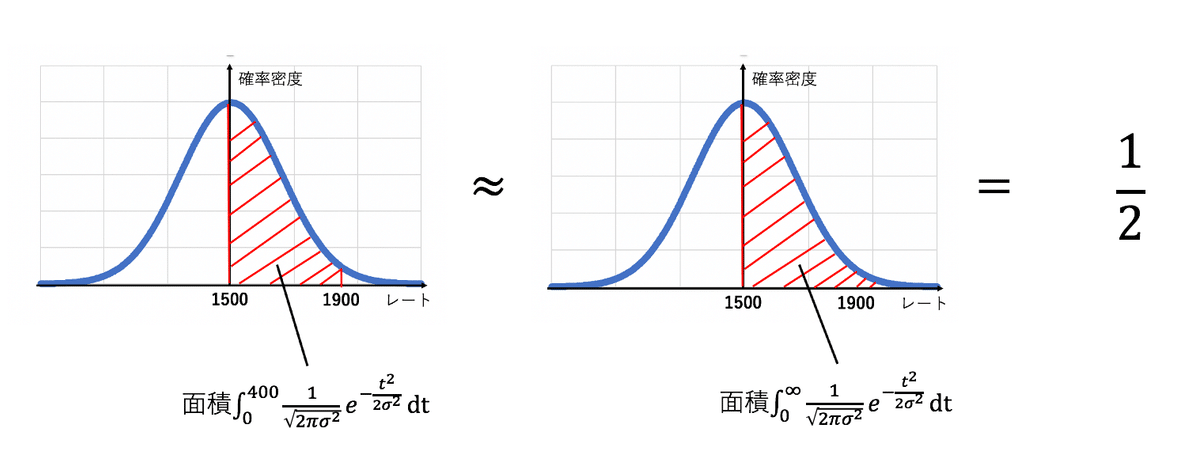
ここで最後の式の第一項目の積分は、正規分布のグラフの真ん中からほぼ右端までの面積なので
$${\int^{400}_{0}\frac{1}{\sqrt{2\pi \sigma^2}}e^-\frac{t^2}{2\sigma^2}dt \approx\int^{\infty}_{0}\frac{1}{\sqrt{2\pi \sigma^2}}e^-\frac{t^2}{2\sigma^2}dt=\frac{1}{2}（ガウス積分）}$$
と近似することができます。（全確率1の半分なので$${\frac{1}{2}}$$とすぐにわかります。）

一項目の積分

よって$${E[\Delta{R}]=\frac{16}{N}[\frac{1}{2}p-\int^{400}_{0}\frac{1}{\sqrt{2\pi \sigma^2}}\frac{1}{1+10^\frac{t-200}{400}}e^-\frac{t^2}{2\sigma^2}dt]}$$

ここで、$${E[\Delta{R}]=0}$$となる時、勝って獲得するレートと負けて失うレートの期待値がちょうど釣り合って長期的にレートが維持できる状態のため、この時の勝率$${p=p_0}$$を釣り合いの勝率と呼ぶことにします。
マスター帯全体のレートの分散を$${\sigma^2}$$とした時、レート1700の時の釣り合いの勝率$${p_0}$$は以上より
$${p_0=2\int^{400}_{0}\frac{1}{\sqrt{2\pi \sigma^2}}\frac{1}{1+10^\frac{t-200}{400}}e^-\frac{t^2}{2\sigma^2}dt}$$
と比較的単純な形で表すことができることがわかりました。

最後に$${\sigma^2}$$の値を考えた上で実際に定積分を行い$${p_0}$$を計算したいのですが、その前にまず分散の値が極端な場合を考えてみます。
具体的には分散がとても小さい場合を考えます。
分散が0の極限ではレート1500に自分以外の全員が集まっていて、自分だけが1700にいるような状態になります（夢のようですね）。
この時は常にレート差$${-200}$$マッチングをするので勝って約$${+4}$$,負けて約$${-12}$$となる（地獄のようですね）ため、だいたい3回勝って1回負ける勝率（75%）でレートを維持できるはずです。

分散が小さい時は1500近傍に集まっています。

実際$${p_0}$$式で例えば$${\sigma^2=1}$$として積分計算をしてみます。この積分は不定積分を初等的な関数で表すことができないためwolfram alphaを用いて数値的に計算しました。
すると$${p_0\approx0.759}$$となりました。「獲得レートの計算式」のところで計算した獲得レートの最大値,最小値を用いると、この時のレートの変動の期待値は大体$${3.84\times0.759-12.16\times0.241\approx-0.016\approx 0}$$なので概ね正しそうですね。

分散1の時の釣り合いの勝率

次に分散がとても大きい時についても考えたいのですが、この時は先ほど計算した$${p_0}$$の標識は使えません。なぜなら、$${E[\Delta{R}]}$$の計算で用いた$${\int^{400}_{0}\frac{1}{\sqrt{2\pi \sigma^2}}e^-\frac{t^2}{2\sigma^2}dt \approx\int^{\infty}_{0}\frac{1}{\sqrt{2\pi \sigma^2}}e^-\frac{t^2}{2\sigma^2}dt}$$の近似が成り立たないからです（レート1900が分布の端っこじゃなくなる）。ただ分散が限りなく大きい時はレートの分布が平らになるため釣り合いの勝率$${p_0=0.5}$$となることが簡単に予想できます。

この時点で実際の釣り合いの勝率は$${p_0=0.5\sim 0.75}$$の間にあると予想はつきます。

分散を極端に大きくすると分布が平らに広がる

マスター帯のレート分布の分散

では実際の$${\sigma^2}$$はどのくらいのものかを考えてみます。
本来はサンプルを収集し区間推定を行ってみたかったのですが、ランダムなレートのサンプルを集めることが困難であったため、以下のようにして（かなり）大雑把な推定をしてみました。（統計は専門ではないのでまずいことをしていたらご指摘いただけると嬉しいです。）

7/31（GENJI カップ最終日）のNDマスター帯の人口を約10000人[8]と仮定します。レート1568で815位という情報を提供していただいた[9]ので、1568以上の割合が$${\frac{815}{10000}=0.0815}$$となるような$${\sigma^2}$$を数値的に求め、それを今回の母分散の推定値とします。
実際に計算すると$${\sigma^2=2375(\sigma\approx49)}$$の時だいたいこれと整合することがわかります。

分散2375の時レート1568以上の割合が約0.0815となる

正規分布では中心から$${\pm\sigma}$$の中に約68%が入ることを考えると、マスター帯の$${\sigma}$$がだいたい50弱くらいというのは、大外れはしてないかなと思います。

レート1700を維持する勝率

では最後に、分散の値を先ほど考えた$${\sigma^2=2375}$$として、レート1700における釣り合いの勝率$${p_0}$$を計算した結果を以下に示します。

分散2375の時のレート1700における釣り合いの勝率

今回の設定上での結果としては勝率71.5%程度あればレート1700を長期的に維持することができるということがわかりました。これはなかなか直感とも一致しているのではないでしょうか。

参考資料等

[1]2022/6 ディアボロスZカップの最終ランキング

[2]2022/7 GENJIカップの最終ランキング

[3]note.「レート1700を目指すにあたって考えたこと」オレンジ　(参照2022/8/10)

[4]WIIS.「イロ・レーティングシステムの意味と求めかたを完全解説」（参照 2022/8/10）

[5]デュエプレ　プラ4星１放置について https://komurokei2025.com/archives/6785
[6]

[7]

[8]

[9]


この記事が気に入ったらサポートをしてみませんか？