
なぜ人は儲かる(かもしれない)のに投資をしないのか:その2 効用
前回までのお話
前回,その1で「なぜ儲かる可能性があるのに,多くの人は投資を行わないのか」という問いを提起しました.
本noteでは,新たに「効用」という概念を導入してこの問いへの一つの説明を与えたいと思います.なお,記号や設定などは前回のノートを踏襲していますので,ぜひ前回をご参照してください.
効用
子どものころ,みなさんはいくらお小遣いをもらっていましたか? 月に500円とか1000円をもらって,お菓子を買ったりして,とても喜んでいたのではないでしょうか.しかし,大きくなって仕事をしてお金を稼げるようになると,お小遣いと同じ額をもらっても(もちろんうれしいはうれしいけれど)子どものころに感じたほどのうれしさは感じないのではないでしょうか.
このうれしさの違いは効用という概念から理解することができます.効用とは「主観的なうれしさ・楽しさ」を数値化したものです.効用が高いほうがよりうれしさを感じている,ということになります.
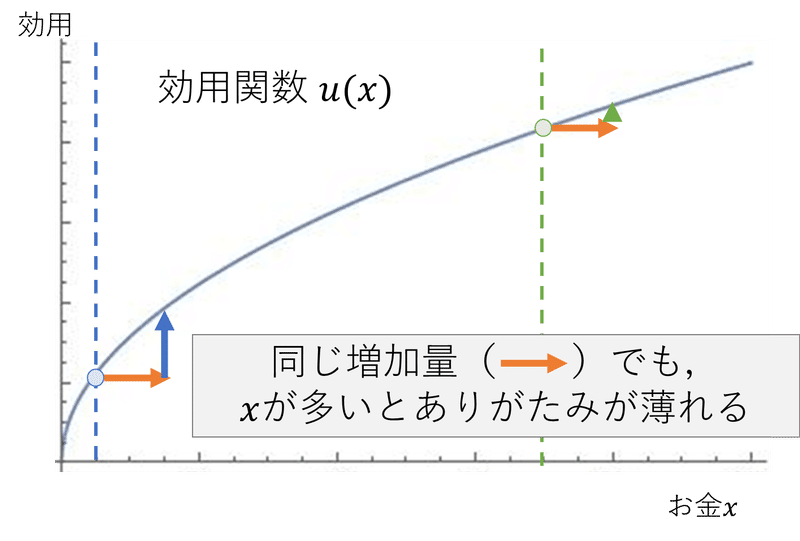
効用の対象が連続的な場合は,効用関数という形で与えられます.たとえば,さきほどの子どものお小遣いを例に考えましょう.「$${x}$$円の資産を持っている」という状況に対するうれしさを$${u(x)}$$で表すことにしましょう.$${u(100万)}$$は「100万円の資産を持っている」という状況に対するうれしさを表します.グラフに書き起こせば図1のような形になります.

単調増加
日常的な感覚を踏まえると,効用関数が一般に満たすべき(こうあってほしい,仮定)特徴が2つあります.まず1つ目は,資産額$${x}$$が増えると効用関数$${u(x)}$$も増える,という特徴です.資産は多いほうがうれしいですよね.1円よりも2円,2円よりも4円,100万円よりも1000万円がうれしいのは人の性です.効用関数はこの人の性質を反映して,次のような不等式を満たすと仮定します.
$$
u(1)<u(2)< \cdots <u(100万)<u(200万)< \cdots .
$$
この仮定は数学的には単調増加と呼ばれています.厳密に書けば次のように表現できます.
$$
x>y ならば u(x)>u(y). 効用関数は単調増加である
$$
つまり,資産額$${x}$$が$${y}$$よりも大きければ($${x>y}$$),$${x}$$を持っているときのほうが$${y}$$を持っているときよりもうれしい($${u(x)>u(y)}$$)ということです.図1の効用関数を見ると,$${x}$$が増加すると(横に進むと)$${u(x)}$$が増加する(グラフの線が上がる)ことがわかります.
限界効用逓減測
2つ目の満たすべき特徴は,資産額が多くなるとお金のありがたみが薄れる,ということです.これは冒頭に説明した,子どもと大人の間の500円の受け取り方の違いを表しています.子どものころは資産を持っていません.たとえば1000円入った財布が子どもにとっての全財産だとしましょう.この状態から500円さらにもらったとき,うれしさの増加分は効用関数$${u(x)}$$を使って次のように表されます.
$$
u(1500)-u(1000). 子どもが500円もらったときのうれしさ増加分
$$
つまり,1500円もっているときのうれしさ$${u(1500)}$$から1000円もっているときのうれしさ$${u(1000)}$$を引けば,500円もらったときのうれしさの増加分になります.$${u(500)}$$ではありませんので,注意が必要です.
一方,大人の場合はそれなりに蓄積があるでしょう.仮に大人になって100万円の資産を持っているとしましょう.このときの500円もらったときのうれしさの増加分は,子どものときの計算を真似して次のように表すことができます.
$$
u(1000500)-u(1000000). 大人が500円もらったときのうれしさ増加分
$$
しかし,いま手元に100万円あるとして,さらに500円もらったところでそんなにうれしくはないですよね.これが「資産額が多くなるとお金のありがたみが薄れる」という状態です.うれしさ増加分の比較をすれば,次のように表されます.
$$
(子どもが500円もらう)>(大人が500円もらう).
$$
効用関数で表すと,次のような形になります.
$$
u(1500)-u(1000)>u(1000500)-u(1000000). ありがたみが薄れる
$$
おなじ500円でもすでに持っている額で増加分が変わります.このような特徴を限界効用逓減則と呼びます.「限界効用」とは,「効用の対象(さきほどの例ではお金)が1単位増えたときの効用の増加分」を指します.この限界効用がじわじわと減少していく,ということをこの法則は表しています(図2参照).
期待効用を計算する
さて,話を株と預金に戻しましょう.人は金額だけで金融商品を選ぶとは限りません.その金融商品が自分に対してどのような「うれしさ」をもたらすか,によって選ぶこともあるでしょう.ということで,効用の観点から株と預金を見直しましょう.
まず,具体的な効用関数を設定します.今回はシンプルに$${u(x)=\sqrt{x}}$$と設定しましょう.これは,先ほど取り上げた2つの特徴(単調増加,限界効用逓減則)を満たす関数です.そして図1, 2は実は$${u(x)=\sqrt{x}}$$を描いています.
株と預金を効用の観点から見直してみましょう.まずわかりやすい預金の方からみてみます.

預金に預けると確実に利息が付き,105万円に資産が増えます.このときの効用は,$${u(x)=\sqrt{x}}$$を使って,次のように計算できます.みなさんも電卓で計算してみましょう.
$$
u(105万)=\sqrt{105万}=\sqrt{1050000} \fallingdotseq 1024.70.
$$
ということで,効用を確率変数$${V}$$で表せば,効用の期待値,つまり期待効用は次のように計算できます.
$$
E(V)=1\times \sqrt{105万}=1 \times 1024.70=1024.70.
$$
続いて株に投資した時の期待効用を計算してみましょう.株に投資した場合は,2つの事象があるので,それぞれの事象での得られる資産に対する効用を計算しましょう.

株価が上昇したときの資産は120万円なので,このときの効用は次の式で計算できます.
$$
u(120万)=\sqrt{120万}=\sqrt{1200000} \fallingdotseq 1095.45.
$$
一方,株価が下降したときの資産は90万円なので,効用は次のように計算されます.
$$
u(90万)=\sqrt{90万}=\sqrt{900000} \fallingdotseq 948.68.
$$
これで2つの事象に対応する効用が得られました.この2つの効用のどちらが得られるかは確率的に変わります.よって,株に投資した時の効用を確率変数$${U}$$として表せば,その期待値$${E(U)}$$は次のように計算されます.
$$
\begin{array}{rl}
E(U) & =0.51\times u(120万)+0.49\times u(90万) \\
& =0.51\times \sqrt{120万}+0.49\times \sqrt{90万} \\
& \fallingdotseq1023.53.
\end{array}
$$
これが,株に投資したときの期待効用という形になります.
効用から見た投資をためらう理由
株と預金,ふたつの期待効用が出そろいましたので,比べてみましょう.
$$
\begin{array}{rl}
株の期待効用: & E(U)=1023.53. \\
預金の期待効用: & E(V)=1024.70.
\end{array}
$$
ならべてみると,期待効用の面では預金に預けるほうが高いことになります.前回のnoteでたてられた問いに戻りましょう.なぜ多くの人々は株に手を出さないのでしょうか.
ありうる理由の一つが期待効用です.確かに期待資産は株のほうが高いのですが($${E(X)>E(Y)}$$),期待効用の観点では預金のほうが高いのです($${E(U)<E(V)}$$).人はより効用の高いほう(よりうれしさの増すほう)を選ぶと想定すれば,効用の高い預金を選び,効用の低い株は選ばれにくい,ということはある意味で自然な帰結ではないでしょうか.
この計算からわかるように人には確実性を好む性質があります.そのような性質を反映した効用関数をリスク回避的な効用関数と呼びます.得られる金額の期待値が同じであっても,確実に得られるほうが確率的な変動がある場合よりも効用が高いことからそう呼ばれます.
なお,この「人はより効用の高いほう(よりうれしさの増すほう)を選ぶ」という想定は期待効用最大化の原則と呼ばれています.この仮定は経済学や社会学(特に合理的選択理論と呼ばれている分野)では人々の行動原理の一つとして位置づけられています.
本noteを読んで社会科学における数理モデルに興味を持った方は,以下の本を読まれることをお勧めします.
私のほうでも数理モデルに関するテキストを作成中ですので,よければご覧ください.
また,関連したnoteも公開中です.
