CourseraWeek8で紛らわしかったところ(K-mean, PCA)

K-mean法

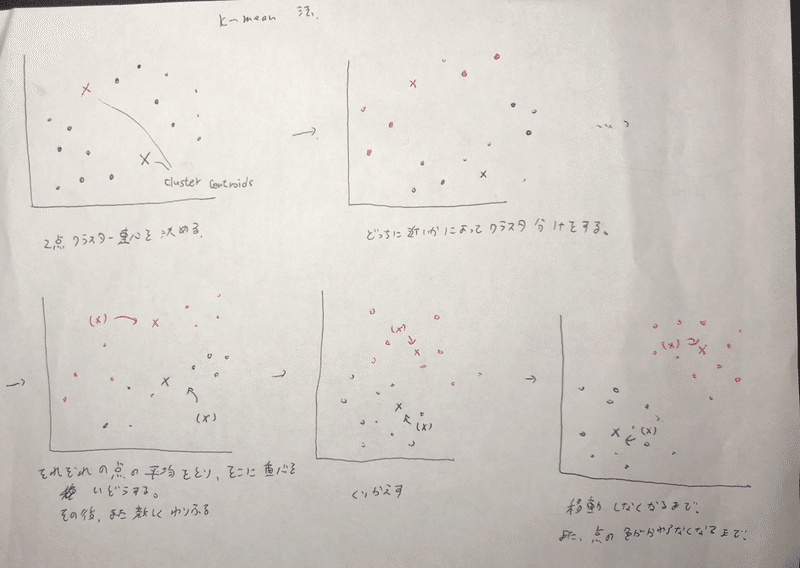
教師なし学習で、クラスタリングの一つ。

１．クラスター重心(centroid)を決める。（上記は２点）

２．どっちのcentroidに近いかで、クラスタ分けをする。

３．それぞれのクラスタの値の平均をとり、その平均の場所にcentroidを移動させる。

1～3を繰り返し、移動しなくなったらおわり。

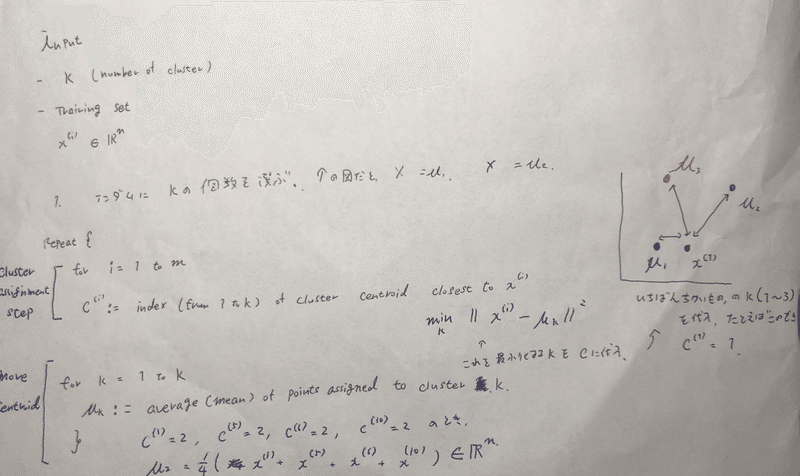
Cluster centroid　を決めるアルコリズムは、、

repeat{

for i = 1 to m

c(i) <- index( from 1 to k ) of cluster centroid closest to x(i) 

つまり、min || x(i) - μ(i)|| をとるKをCに代入する。（K= μ(1),μ(2),,,,,,)

上の右の方の図だと、x(1)は、μ(1)にもっとも近いので、c(1) = 1 となる。

また、cluster centroid を動かすステップのアルコリズムは、、

for k = 1 to k  

μ(n) <- average(mean) of points assigned to cluster K.

}

たとえば、C(1)=2, C(5)=2, C(6)=2, C(10)=2 だった時、

μ(2) <- 1/4 *( x(1) + x(5) + x(6) + x(10) )

ちなみに、

C(i) = x(i)がどのクラスターに分けられているか表す。

μk = クラスターKの場所を表す。

μc(i) = x(i)に割り振られている（x(i)を囲んでいる）クラスターを表す。

また、目的関数は、

J = ( C(1)~C(m), μ(1)~μ(k)) = 1/m * || x(i) - μc(i)||^2

であり、c (1~m), μ(1~k)をトレーニングする。（出す）

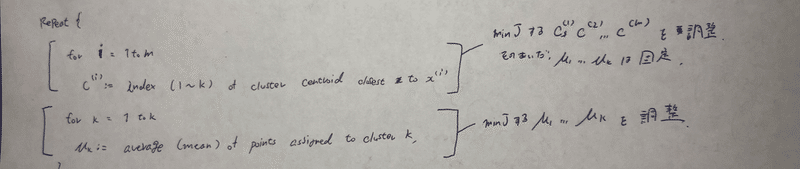
アルコリズムの中で同時にCとμを計算するのではない。

repeat{

for i = 1 to m

 c(i) <- index(1 ~ k) of cluster centroid closest to x(i)   

Cluster centroid を移動させるステップで、minJするc(1~m)を調節。その間μ(1~k)は固定。

for k = 1 to k

μk <- average (mean) of points assigned to closest k 

Cluster centroid をクラスターの平均に移動させるステップでminJするμ(1~k)を調節。

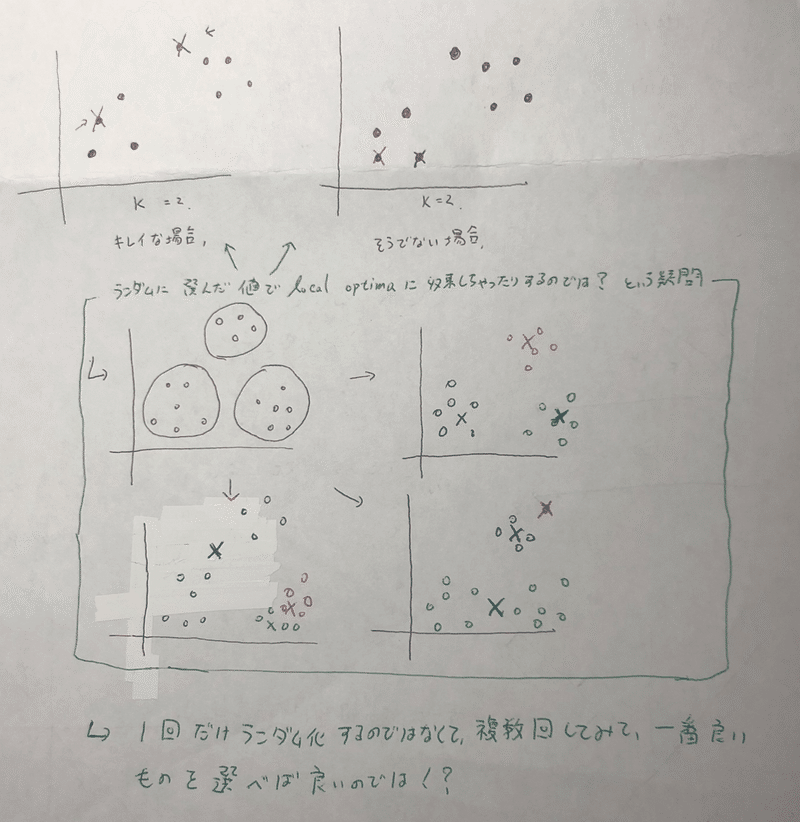
てか、キレーに点が分かれていたらいいけど、そうでない場合は Local optimaに収束しちゃわないか？という疑問が出る。実際ローカルな値に収束してしまうことがある。

→では、initialの値を一回だけランダム化してアルコリズムを回すのではなく、複数のinitialの値でアルコリズムを回してみて、一番良いものを採用しようではないか。

これがそのアルコリズム。

for i = 1 to 100 {

Randomly initialize K-means,

Run K-means , Get C(1~m), μ(1~K),

Compute cost function J 

}

100回、回しているから、100個のJが得られる。その後一番小さい値のJを選ぶ。

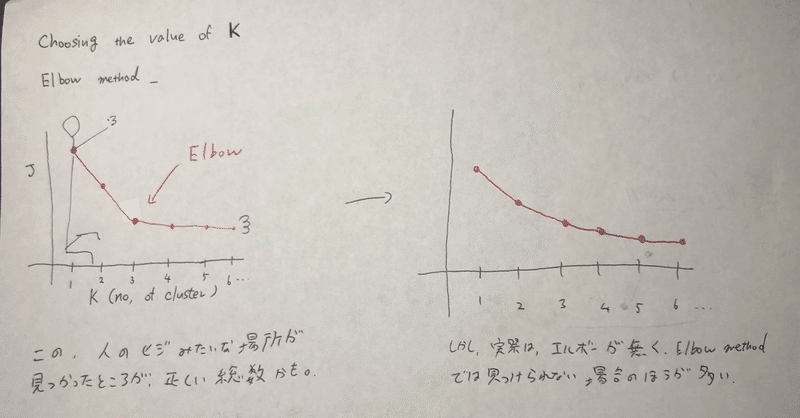
で、クラスター数（number of k) どうするよという疑問が生まれる。

Elbow method というものが存在する。Kの個数をｘ軸、Jをｙ軸にプロットして、ニンゲンの肘レベルで折れ曲がっているところがあれば、そこが最適なｋの個数カモね。

・・だけど、現実にはエルボーが存在することは稀で、あまりElbow method は使われない。

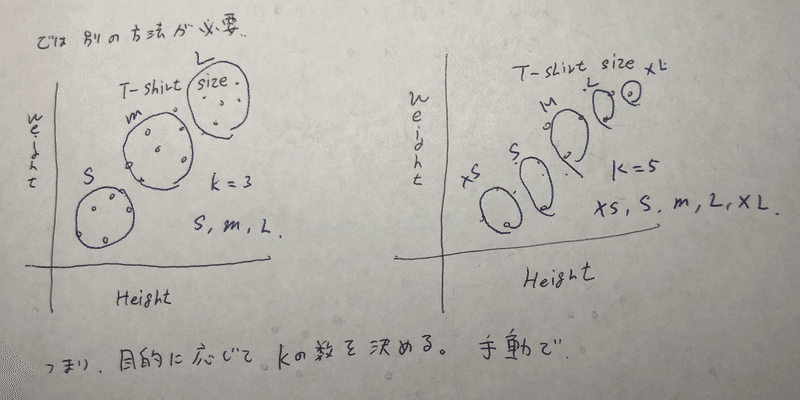
じゃあ実際どうやってｋの個数を決めているか。

現在のところ、高度なアルコリズムはなく、実際の（ビジネスなどの）目的によって決めている。

たとえば、TシャツのサイズをS、M、Lと三分割したければ、ｋの個数は３だし、ｘｓ、ｓ、ｍ、ｌ、ｘｌとしたければｋは５つ必要である。

→目的に応じて主観的にｋの個数を決める

PCA_____

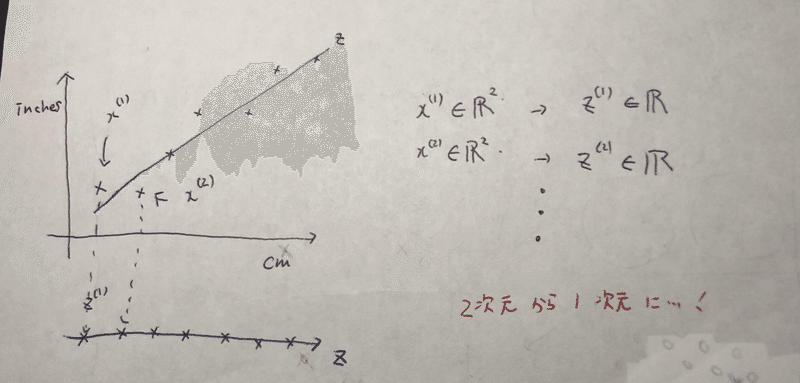
PCA とは、次元を下げるメソッド。

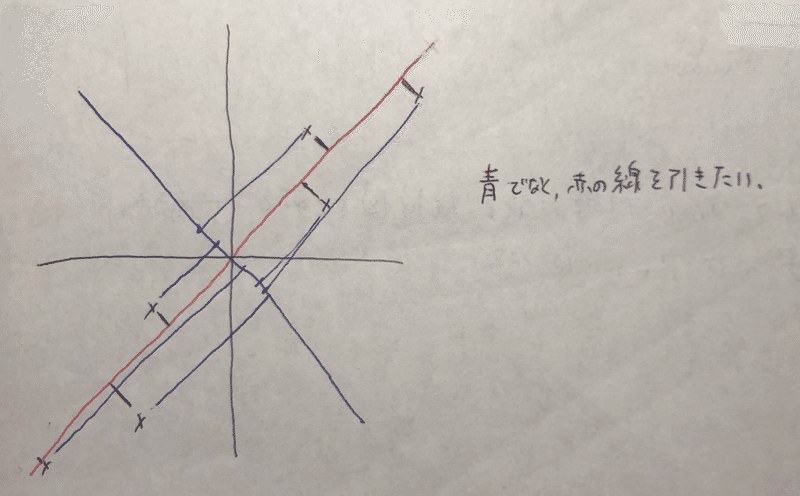
青の線でなく、赤の線を引きたい。つまり、それぞれの距離がminとなるような線を選びたい（最小二乗法的な・・？）

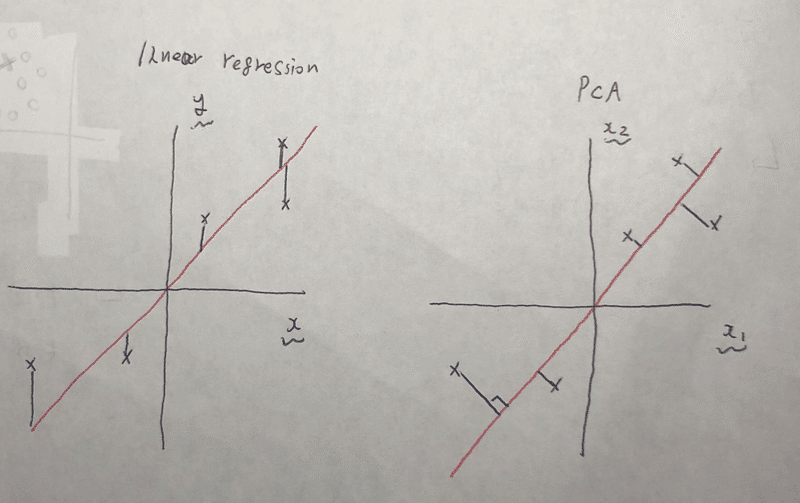
ただ、最小二乗法とは全く違うアルコリズムである。

図的に説明すると、左が最小二乗法で右がPCA。

また、最小二乗法ではｘ、ｙ軸があるのに対して、PCAはｘ１、ｘ２軸しかない。つまり、最小二乗法はｙの予測を念頭に置いているが、PCAは目的変数などない。根本から違うアルコリズムである。

また、PCAを行う際は、必ずヒューチャースケーリングを行う必要がある。

PCAの流れとしては（ノート取ってない・・）

１．Σ（共分散行列）を計算する　（sumではない、注意)

２．Σ（共分散行列）の固有ベクトルを計算する。

３．計算した固有ベクトルを用いてｎ次元からｋ次元に圧縮したベクトルｚを計算する。

１．Σ（共分散行列）の計算。

Σ = 1/m * Σ(1~m) {x(i) * x(i)'}

vector ver..

Sigma = (1/m) * X' * X

２．共分散行列Σの固有ベクトルを計算する。

[U, S, V] =svd(Sigma)

ちなみにUが固有ベクトル。Σと同様ｎ＊ｎ行列。

３．Uの最初のｋ列を取り、ｎ次元からk次元に圧縮したベクトルｋを計算する。

z(i) = U_reduce' * x(i)

U_reduce'はｋ＊ｎ行列で、ｘがｎ＊１行列だから、ｚはｋ＊１行列になる。

コードだと、

Ureduce = U( : , 1:k )

Z = X * Ureduce

ここまで一気にまとめると、、

Sigma = (1/m) * X' * X       共分散行列を求める

[U, S, V] = U( : , 1:k ) 　　固有ベクトルを求める

z = X * Ureduce 　　　　圧縮したｚを出す。

圧縮したｋ次元からｎ次元に戻すには＿＿

z(i) = Ureduce' * x(i)  だから

x(l)_approx = Ureduce * z(l)

いくつの次元まで圧縮するか＿＿圧縮する次元数の決め方

二乗射影誤差と全体の分散の比率を取って何％未満とする（たとえば、1%未満なら、９９％の主成分が保持されていることになる）

１．1/m Σ(1~m) { || x(i) - x_approx(i) ||^2} ...①　二乗射影誤差を求める

２．1/m Σ(1~m) { || x(i) || ^2 } ...②　全体の分散を求める。

３．① / ②　<= 0.01 を満たす最小のｋ次元を求める。

具体的には、

[ U, S, V ] = svd(Sigma) を呼び出し、Sを用いる。

Σ(1~k) Sij / Σ(1~n) Sij >= 0.99 を満たす最小のｋを求める。当てはまらなければ少しずつｋの値を増やしていく。

PCAを使うときに気を付けること＿＿

PCAはトレーニングセットにのみ行う。PCAの主な用途は、次元を減らすことでのスピードアップ、メモリの削除、データの可視化（２、３次元のグラフを描くため）である。したがって、次元を減らすことによる over fitting を均すために使用するのは間違った使い方。あくまでもover fitting を防ぐなら正則化を使う。

課題＿＿

１．findClosestCentroids

FINDCLOSESTCENTROIDS computes the centroid memberships for every example
 idx = FINDCLOSESTCENTROIDS (X, centroids) returns the closest centroids
 in idx for a dataset X where each row is a single example. idx = m x 1
 vector of centroid assignments (i.e. each entry in range [1..K])  らしいです。

idx にそれぞれのデータに最も近いcentroidを保存させるらしいです。

function idx = findClosestCentroids(X, centroids)

K = size(centroids, 1)

idx = zeros(size(X,1),1)

for i = 1 : size (X, 1)

 min_c = inf

 for j =1 : K

 c  =(X( i ,: ) - centroids( j ,: )) * (X( i , : ) - centroids( j , : ))'

   if c <= min_c

    min_C =c

  idx(i) = j

end

end

end

２．computeCentroids

それぞれのクラスターの平均値を出し、centroidsを移動させていくステップです。

function centroids = computeCentroids(X, idx, K)

[m n] =size(X)

cemtrpods = zeros(K, n)

---- your code here----

for k = 1:K
　sum_X = zeros(1,n);
　count = 0;
　for i = 1:m
　　if idx(i) == k
　　sum_X(1,:) = sum_X(1,:) + X(i,:);
　　count = count + 1;
　end
end
mean_X = 1/count*sum_X;
centroids(k,:) = mean_X;
end

３．kMeansInitCentroids

最初のcentroidsを決めます。

１．training exampleをランダムに並び替え

２．最初のｋ個をinitial centroids に

function centroids = kMeansInitCentroids(X, K)

centroids = zeros ( K, size(X,2))

---your code here---

random_idx = randperm(size(X, 1))      １．ランダムに並び替え

centroids = X(random_idx(1 : k ), :)　　２．最初のｋ個をとる

 

4．pca

XでPCAを回す課題です。そのまま。

function [U, S] = pca(X)

[m , n] = size(X)

U = zeros(n)

S = zeros(n)

---your code here---

Sigma = 1/m * (X)' * X

[U, S, V] =svd(Sigma)

5．project data

Uの最初のｋ個を取ってPCAを回します。

function Z = projectData( X, U, K)

Z = zeros (size(X, 1), K)

--- your code here----

U_reduce = U( : , 1 : K ):   

Z = X * U_reduce:

end

６．recoverData

5で作ったｚをもとに戻します。

function X_rec - recoverData (Z, U, K)

X_rec = zeros(size(Z, 1), size(U, 1))

---your code here--

for i = 1 : size(U,1)
X_rec( : , i ) = Z * U( i , 1:K )'
end