
Eigenと自分のライブラリの行列計算時間を比べてみた
2024/11/06 実施
目的
以下のリアルタイム制御向け行列ライブラリ「python_numpy_to_cpp」の計算時間を評価します。ライバルのEigenと勝負です。
Modeling-Coding-Automation-Project/python_numpy_to_cpp: リアルタイム制御向けC++行列ライブラリです。
Eigenのバージョンは3.4.0を用いました。
計測対象の実機
Arduino Dueを使います。
MCU(マイクロコントローラ): AT91SAM3X8E(ARM Cortex-M3)
クロック周波数: 84 MHz
SRAM: 96 KB(64 KBと32 KBの2バンク)
プログラム格納用フラッシュメモリ: 512 KB
IDEはVisual Studio Codeで、PlatformIOを用いました。
テスト1: 行列積
4行4列の行列積を計算し、その計算時間を比較しました。
python_numpy_to_cppの行列積
PythonNumpy::Matrix<PythonNumpy::DefDense, float, 4, 4> A(
{{2, 3, 1, 5}, {4, 1, 6, 2}, {0, 7, 3, 8}, {9, 5, 2, 4}});
unsigned long time_start = 0;
unsigned long time_end = 0;
/* calculation */
time_start = micros(); // start measuring.
auto D = A * A;
time_end = micros(); // end measuring.この計算をする以外は最低限のコード量で、上記コードはマイコン起動開始時に1度だけ実行します。他の余計な処理は可能な限り排除しています。
ビルドすると、RAMとFlashは以下の通りです。これだけ大量に消費するのは、おそらくC++の標準ライブラリを読み込んでいるせいかな、と思っています。

実行結果は以下の通りです。
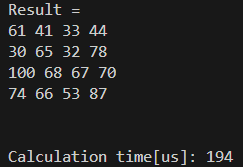
答えは合っています。194usもかかりましたね。FPUが存在していないので、仕方ないかなと思いました。
Eigenの行列積
同じように、Eigenの計算時間を計測します。
Eigen::Matrix<float, 4, 4> A;
A << 2, 3, 1, 5, 4, 1, 6, 2, 0, 7, 3, 8, 9, 5, 2, 4;
unsigned long time_start = 0;
unsigned long time_end = 0;
/* calculation */
time_start = micros(); // start measuring.
Eigen::Matrix<float, 4, 4> D = A * A;
time_end = micros(); // end measuring.結果は以下の通りです。

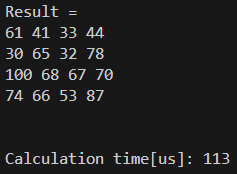
RAM, Flashは変わりませんが、計算時間が0.58倍、早い!
完全に負けましたが、いくら何でも早すぎないか、と思いました。
for文を省いてみる
私のライブラリでは、愚直にfor文を使って計算しています。ちょっと気になったので、for文の負荷を省いたらどうなるか、試してみました。
PythonNumpy::Matrix<PythonNumpy::DefDense, float, 4, 4> D;
D.matrix(0, 0) =
A.matrix(0, 0) * A.matrix(0, 0) + A.matrix(0, 1) * A.matrix
(1, 0) +
A.matrix(0, 2) * A.matrix(2, 0) + A.matrix(0, 3) * A.matrix
(3, 0);
D.matrix(0, 1) =
A.matrix(0, 0) * A.matrix(0, 1) + A.matrix(0, 1) * A.matrix
(1, 1) +
A.matrix(0, 2) * A.matrix(2, 1) + A.matrix(0, 3) * A.matrix
(3, 1);
D.matrix(0, 2) = ...結果は以下の通りです。

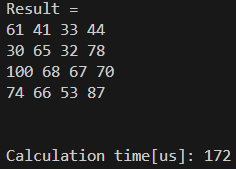
12%削減できました!
やっぱり意外とfor文の計算負荷が効くようですね。しかし、Eigenの速度には及びません。
Eigenのソースコードを読めばいいのですが、かなりややこしいので全部読み解けません。軽く調べてみたところ、おそらく、アセンブラマクロによる積和算計算を置換しているか、ARMの固有ライブラリを使っているのではと思います。
「std::array」を使ってみる
実は、私のライブラリでは「std::vector」を使っているのですが、「std::array」を使う手もあります。
私が「std::vector」を使っているのは、行列は大量のメモリを使うので、できる限りヒープに置いておきたい、という理由からです。「std::array」を使うと、効率は良いのですがスタックを消費するので、メモリに気を使わないといけません。
「std::array」を使うとどうなるか、気になりましたので、試してみました。
std::array<std::array<float, 4>, 4> A;
A[0] = {2, 3, 1, 5};
A[1] = {4, 1, 6, 2};
A[2] = {0, 7, 3, 8};
A[3] = {9, 5, 2, 4};
unsigned long time_start = 0;
unsigned long time_end = 0;
/* calculation */
time_start = micros(); // start measuring.
std::array<std::array<float, 4>, 4> D;
D[0][0] = A[0][0] * A[0][0] + A[0][1] * A[1][0] + A[0][2] * A[2][0] +
A[0][3] * A[3][0];
D[0][1] = A[0][0] * A[0][1] + A[0][1] * A[1][1] + A[0][2] * A[2][1] +
A[0][3] * A[3][1];
D[0][2] = ...結果は以下の通りです。

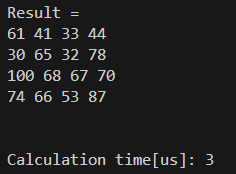
早い!!!!!!
Eigenどころか、それをはるかに上回る速度がでました😅
何かの間違いかと思いましたが、そうでもなさそうです。ここまで違うとさすがに「std::array」を使う実装が欲しくなりましたので、実装してみようと思います。
(次の節で説明しますが、これはおそらくコンパイル時に計算済みの数値がstd::array変数に格納されているのでは、と思いました。なので、std::arrayを使ったからと言って、必ずしもここまで早くはならないと思われます)
テンプレートメタプログラミングにより、for文をコンパイル時に展開する
もちろん、毎度for文をベタ書き展開することなどできませんので、C++のテンプレートメタプログラミングにより、for文をコンパイル時に展開することにします。行列クラスの内部変数はstd::arrayを用いるように修正しました。
/* Compiled Matrix Multiplier Classes */
// when K_idx < K
template <typename T, std::size_t M, std::size_t K, std::size_t N,
std::size_t I, std::size_t J, std::size_t K_idx>
struct MatrixMultiplierCore {
static T compute(const Matrix<T, M, K> &A, const Matrix<T, K, N> &B) {
return A(I, K_idx) * B(K_idx, J) +
MatrixMultiplierCore<T, M, K, N, I, J, K_idx - 1>::compute(A, B);
}
};
// when K_idx reached 0
template <typename T, std::size_t M, std::size_t K, std::size_t N,
std::size_t I, std::size_t J>
struct MatrixMultiplierCore<T, M, K, N, I, J, 0> {
static T compute(const Matrix<T, M, K> &A, const Matrix<T, K, N> &B) {
return A(I, 0) * B(0, J);
}
};
// After completing the J column, go to the next row I
template <typename T, std::size_t M, std::size_t K, std::size_t N,
std::size_t I, std::size_t J>
struct MatrixMultiplierColumn {
static void compute(const Matrix<T, M, K> &A, const Matrix<T, K, N> &B,
Matrix<T, M, N> &result) {
result(I, J) = MatrixMultiplierCore<T, M, K, N, I, J, K - 1>::compute(A, B);
MatrixMultiplierColumn<T, M, K, N, I, J - 1>::compute(A, B, result);
}
};
// Row recursive termination
template <typename T, std::size_t M, std::size_t K, std::size_t N,
std::size_t I>
struct MatrixMultiplierColumn<T, M, K, N, I, 0> {
static void compute(const Matrix<T, M, K> &A, const Matrix<T, K, N> &B,
Matrix<T, M, N> &result) {
result(I, 0) = MatrixMultiplierCore<T, M, K, N, I, 0, K - 1>::compute(A, B);
}
};
// proceed to the next row after completing the I row
template <typename T, std::size_t M, std::size_t K, std::size_t N,
std::size_t I>
struct MatrixMultiplierRow {
static void compute(const Matrix<T, M, K> &A, const Matrix<T, K, N> &B,
Matrix<T, M, N> &result) {
MatrixMultiplierColumn<T, M, K, N, I, N - 1>::compute(A, B, result);
MatrixMultiplierRow<T, M, K, N, I - 1>::compute(A, B, result);
}
};
// Column recursive termination
template <typename T, std::size_t M, std::size_t K, std::size_t N>
struct MatrixMultiplierRow<T, M, K, N, 0> {
static void compute(const Matrix<T, M, K> &A, const Matrix<T, K, N> &B,
Matrix<T, M, N> &result) {
MatrixMultiplierColumn<T, M, K, N, 0, N - 1>::compute(A, B, result);
}
};
#define BASE_MATRIX_COMPILED_MATRIX_MULTIPLY(T, M, K, N, A, B, result) \
MatrixMultiplierRow<T, M, K, N, M - 1>::compute(A, B, result);
/* Matrix Multiplication */
template <typename T, std::size_t M, std::size_t K, std::size_t N>
Matrix<T, M, N> operator*(const Matrix<T, M, K> &A, const Matrix<T, K, N> &B) {
Matrix<T, M, N> result;
// for (std::size_t i = 0; i < M; ++i) {
// for (std::size_t j = 0; j < N; ++j) {
// T sum = 0;
// for (std::size_t k = 0; k < K; ++k) {
// sum += A(i, k) * B(k, j);
// }
// result(i, j) = sum;
// }
// }
BASE_MATRIX_COMPILED_MATRIX_MULTIPLY(T, M, K, N, A, B, result);
return result;
}難しいテクニックなので、解説は省略しますが、コンパイラがコードをコンパイルするときに、上記のMatrixMultiplierCoreなどのテンプレートを解釈し、処理内容を展開します。
結果的に、for文の中の処理をベタ書きすることに等しい実装が得られます。よって、for文の条件処理やインデックスの加算処理が省略できます。
これを使ってみると、結果は以下の通りでした。

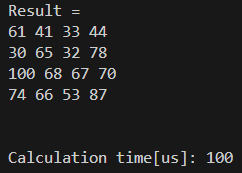
計算時間は100usでした。前の節の3usという結果は、やはり異常なほど早いですね。本当にベタ書きすると、何らかのコンパイラ最適化が働いて高速化できるのだと考えられます。
いずれにしても、結果は100usであり、Eigenに勝ちました!
スパース行列の計算時間を評価(2024/11/23)
同じように、スパース行列と密行列の行列積の計算時間を評価しました。
密行列Aは、先程と同じく
[2, 3, 1, 5]
[4, 1, 6, 2]
[0, 7, 3, 8]
[9, 5, 2, 4]です。
スパース行列Cは、密行列で書くと
[0, 0, 5, 0]
[7, 0, 0, 0]
[4, 0, 0, 3]
[2, 0, 8, 0]である行列です。
この二つの行列の積「C * A」を計算します。
結果は以下の通りでした。

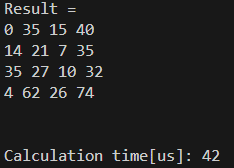
ちゃんと早い結果となりました。
