魔改造メタボール

2021年11月8日 10:04

この記事は想像で書いてます。

この記事はprocessingで書いてます。

良く知られたメタボールは陰関数曲面がなんちゃらかんちゃら、f(x,y)=0なりf(x,y,z)=0なる点の集合とかなんとか言われておることでしょう。
学校で習うy=f(x)なるやつは、入力1個で出力1個。横軸に入力をとって縦軸に出力をとれば簡単にグラフにできるしプログラムに落とし込むのも容易です。
z=f(x,y)ならば、これは3Dになって、プログラム的に表示するのはおっくうだけれども、どういうグラフか想像するのは可能な範囲のものごとであります。
f(x,y)=0などという類のものは、z=f(x,y)なる関数が3Dの山なり谷なりを成すのであれば、それを横なぎ一閃にぶった切って表れたるは切り株断面。それを２次元平面にうっちゃって、えいやとばかりに魚拓をとった関数の輪郭とでもいうべきもので、
これをプログラム的に素直に表示を試みるとなると、縦横にグリッド切って、そのグリッドの交点毎にf(x,y)を出力せしめて、if(z==0)なるかを見るというような、極めてやりづらいやつになるのであります。

最も単純な実装は、ピクセルごとに走査して、ピクセル単位で色を塗る、塗らないを決定するようなやり方で、

void fxy()
{
    for(int i = 0; i<height; i++)
    {
        for(int j = 0; j<width; j++)
        {
            var z = func(x,y);
            if(threshold<z)
            {
                plot(x,y);
            }
        }
    }
}

なる体をなすことでしょう。

2次元的なメタボールは、2次元平面上にメタボールをいくらかとって、内部でそれらを用いたfunc(x,y)を計算することによりピクセル単位で描画することが可能になります。

しぬほど大雑把な実装。

void setup()
{
 size(500,500);
}

void draw()
{
 background(255);
 
 var m1 = new PVector(180,200);
 var m2 = new PVector(320,200);
   
 loadPixels();
 for(int i = 0; i<height;i++)
 {
   for(int j = 0; j<width; j++)
   {
     double f = metaball_func(m1,m2,j,i);
     if(f>0.00025)
     {
       pixels[i*width+j]=color(0);
     }
   }
 }
 updatePixels();  
}

double metaball_func(PVector m1, PVector m2, int x, int y)
{
 double f1 = 1/(double)((x-m1.x)*(x-m1.x)+(y-m1.y)*(y-m1.y));
 double f2 = 1/(double)((x-m2.x)*(x-m2.x)+(y-m2.y)*(y-m2.y));
 return f1+f2;
}

これでは使いづらいので改造します。

初期の研究では

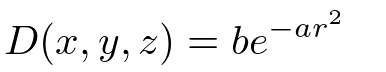
なる関数を用いていたらしく、２次元ならD(x,y)。

参考

これが結局、座標 (j,i) に対するメタボール1つ分であって、メタボールがN個あるなら、座標 (j,i) において上の関数がN個分加算されるわけです。

空間中のすべての点が、空間中に存在するすべてのメタボールからそれなりに影響を受ける。

メタボールから離れるとメタボールの影響力は薄れる。

それを踏まえた上で式を見ますと、
上の式のうち、rというのがメタボールと座標 (j,i) との距離。

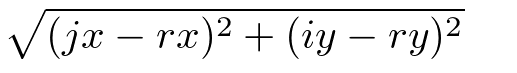
なるピタゴラスであって、ベクトル的には(j,i)-rないしr-(j,i)の長さ。processing的には

(PVector.sub(new PVector(j,i), new PVector(metaball.x,metaball.y))).mag()

eというのはネイピア数e = 2.71828 18284 59045...なるヤベー数で、こいつについて考えだすと頭がおかしくなるので飛ばしますが、

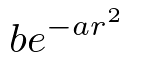
なるは全部合わせてガウシアンを半分こしたやつだと知られています。

しぬ程強引なガウシアン

wikipediaにのってるガウシアン

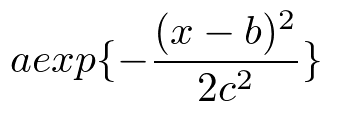
なる式のうち、
a=1,b=0,
1/2c^2なるをまとめて1になるようにcを調整すると、ガウシアンのガウシアンたるゆえんはexp(-x*x)の部分のみ。

exp(0)、すなわちeの0乗で1となり、これが出力の最大値です。
eのマイナスなんちゃら乗は、分母をなんちゃら乗するため、eのなんちゃら乗分の1となり爆裂的に0に近づきます。

なので出力はだいたい0から1です。
パラメータを削り殺したガウシアンは入力を-3から+3くらいまでとり、-3より小さい数、あるいは+3より大きい数の入力は計算が爆散します。プログラミング的にはもう少し早めに爆散します。

import java.util.List;

List<Float> glist = new ArrayList<Float>();

void setup()
{
 size(500,500);
   
 for(int i = 0; i<width; i++)
 {
   var g = gauss(map(i,0,width,-3,3));
   glist.add(g*height/2);     
 }
}

void draw()
{
 background(255);
 for(int i = 0; i<glist.size(); i++)
 {
   line(i,0,i,glist.get(i));
 }
}

float gauss(float x)
{
 return exp(-x*x);
}

メタボールと座標 (j,i) との距離rは負値をとりませんので、入力は0から+3となりましょう。ガウシアンの半分ことはそういう意味です。

var g = gauss(map(i,0,width,0,3));

exp(-x*x)じゃない場合を見ましょう。

float gauss(float x)
{
 return exp(x*x);
}

入力を2乗しないなら、普通の指数関数。

float gauss(float x)
{
 return exp(-x);
}

float gauss(float x)
{
 return exp(x);
}

線分メタボール

以上を踏まえた上で、関数f(x)を使うような感覚で以下のようなものが使えると便利です。

これは2つのメタボールを繋いだというか、線分の両端にメタボールを接続したというか、そんなようなものです。

a=10の場合

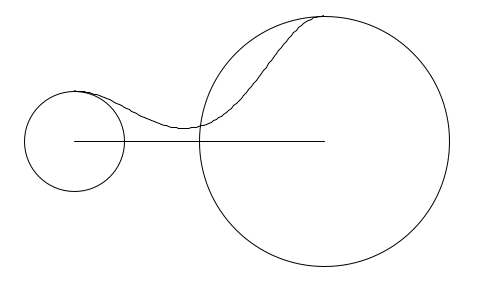
expの出力が0から1でしたので、以下の関数

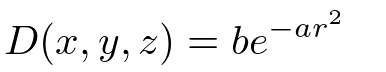
のb部分がメタボールの半径だと考えるとなんかうまいこといきそうな気がします。rは距離でしたが、expが爆散するしないを気にしながらチマチマ関数をいじくるのは面倒です。線分というのは0-1で線分上の位置を示せましたので、rも0-1しかとらないと決めてしまいます。勝手なことしたゆがみを、とりあえず係数aに押し付けます。ガウシアンが爆散するしないはaのいかんにかかります。

float MetaballLineSpline_t(PVector sv, PVector ev, float r1, float r2, float a1, float a2, float t)
{
 var lv = ev.copy().sub(sv);
 var lv_nag = VectorMethod.Nagate(lv);   
 
 //rを0-1に
 var total_len = lv.mag();  
 var sx =lv.copy().mult(t).mag()/total_len;
 var ex =lv_nag.copy().mult(1-t).mag()/total_len;  
 
 //メタボール毎にD(x,y)を求める。実際はD(t)になっている。
 var e1 = r1*exp(-a1*sx*sx);
 var e2 = r2*exp(-a2*ex*ex);   
 var ret = e1+e2;   
 return ret; 
}

static PVector Nagate(PVector v)
{
 return new PVector(-v.x,-v.y);
}

上の関数を線分に渡って適用する。

List<PVector> MetaballLineSplineL(
 PVector sv, PVector ev, float r1, float r2, float a1, float a2, float resolution)
{
 List<PVector> ret = new ArrayList<PVector>(); 
 var lv = ev.copy().sub(sv);
 var lv_left_normal = VectorMethod.TurnL(lv).normalize();
 for(float i = 0; i<1; i+=resolution)
 {
   var proj_pos = sv.copy().add(lv.copy().mult(i));  
   var val = MetaballLineSpline_t(sv,ev,r1,r2,a1,a2,i);
   var v = proj_pos.copy().add(lv_left_normal.copy().mult(val));
   ret.add(v);
 }
 return ret;
}

a=100の場合。メタるのが早いのがわかる。

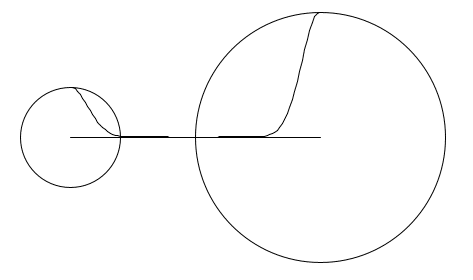
2次元平面上にあるメタボールが線分空間に影響を及ぼす場合

メタボールが線分外に存在する場合を考えます。

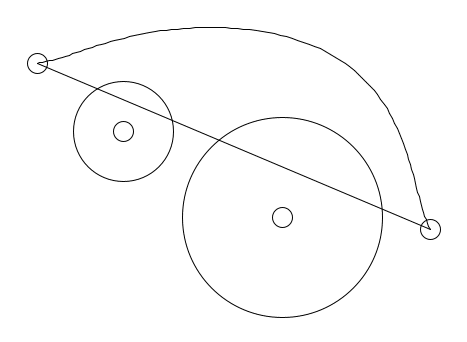
線分上の１点とメタボールとの距離をガウシアンに入力していきます。
得られた距離を線分長で割ることの妥当性は良く分かりませんし、いらんことしてるかもしれませんが、なんかうまいこといってるので良しとします。

メタボール側の円周長で割ってみてもいいかもしれません。

追記：今のところ、total_len =メタボール半径とすることが一番理にかなっていると思われます。

float MetaballSpline_t(
 PVector sv, PVector ev, PVector metaball_center, float metaball_radius, float a, float t)
{
 var lv = ev.copy().sub(sv);
 var total_len = lv.mag();    
 var proj_pos = sv.copy().add(lv.copy().mult(t));    
 //入力値(直線上の１点と円の中心との距離）
 var sx = metaball_center.copy().sub(proj_pos).mag()/total_len;    
 //補間関数
 var ret = metaball_radius*exp(-a*sx*sx);   
 return ret;    
}

上の関数を線分に渡って適用します。

List<PVector> MetaballSplineL(
 PVector sv, PVector ev, PVector circle_center, float circle_radius, float a, float resolution)
{
 List<PVector> ret = new ArrayList<PVector>();  
 var lv = ev.copy().sub(sv);
 var nlv = VectorMethod.TurnL(lv).normalize();  
 for(float i = 0; i<1; i+=resolution)
 {
   float fx = MetaballSpline_t(sv,ev,circle_center,circle_radius,a,i);
   PVector proj_pos = sv.copy().add(lv.copy().mult(i));
   PVector v = proj_pos.copy().add(nlv.copy().mult(fx));
   ret.add(v);
 }   
 AttachSegmentRefTSR(sv,ev,ret);
 return ret;
}

上記の関数を素直に適用すると、出力結果は線分の始点終点から外れます。

それはそれでかまわないのですが、始点と終点がそろっとってほしい場合は補正する必要があります。元の線分の始点終点と、出力結果の始点終点を見比べて、回転拡大縮小平行移動を行えば出力結果は線分の始点終点にピタリと張り付くはずです。

以下、しぬ程強引な補正処理。このページの全てにいえることですが、スマートな方法は他にたくさんあるでしょう。

void AttachSegmentRefTSR(PVector psv, PVector pev, List<PVector> polyline)
{
 var sv = polyline.get(0).copy();
 var ev = polyline.get(polyline.size()-1).copy();
 var tsr = GetTSR(psv,pev,sv,ev);  
 PVector offset = null;
 for(int i = 0; i<polyline.size(); i++)
 {
   var v = polyline.get(i);    
   v.div(tsr.Scale);
   VectorMethod.RotRadianRef(v, tsr.Rotate);
   if(i==0){offset=psv.copy().sub(v);}      
   v.add(offset);
 }
}
class TSR
{
 PVector Offset;float Scale;float Rotate;  
 TSR(PVector offset, float scale, float rotate){
   this.Offset=offset.copy();this.Scale=scale;this.Rotate=rotate;}
}
TSR GetTSR(PVector psv, PVector pev, PVector sv, PVector ev)
{
 PVector plv = pev.copy().sub(psv);
 PVector lv = ev.copy().sub(sv);  
 PVector offset = psv.copy().sub(sv);
 float scale = lv.mag()/plv.mag();
 float rot = VectorMethod.CalcuAngleRadian360(lv,plv);  
 return new TSR(offset,scale,rot);
}
 static void RotRadianRef(PVector v, double radian)
 {
     float x = v.x * cos((float)radian) - v.y * sin((float)radian);
     float y = v.x * sin((float)radian) + v.y * cos((float)radian);
     v.x = x;
     v.y = y;
 }
   static float CalcuAngleRadian360(PVector v1, PVector v2)
 {
   float s = Sin(v1,v2);
   float c = Cos(v1,v2);  
   if(0<s)
   {
     return -(float)Math.atan2(v1.y * v2.x - v2.y * v1.x, v1.x * v2.x + v1.y * v2.y);
   }
   else if(s<0)
   {
     return 2*PI-(float)Math.atan2(v1.y * v2.x - v2.y * v1.x, v1.x * v2.x + v1.y * v2.y);   
   }
   else
   {    
     if(0<c){return 0;}//前    
     else{return PI;}//後      
   }
 }  
   static float Sin(PVector v1, PVector v2)
 {
     float ll = v1.mag() * v2.mag();
     if (ll == 0) { return 0; }
     return Cross(v1, v2) / ll;
 }
   static float Cos(PVector v1, PVector v2)
 {
     float ll = v1.mag() * v2.mag();
     if (ll == 0) { return 0; }
     return Dot(v1, v2) / ll;
 }
   static float Cross(PVector v1, PVector v2)
 {
     return (v1.x * v2.y - v1.y * v2.x);
 }
   static float Dot(PVector v1, PVector v2)
 {
     return (v1.x * v2.x + v1.y * v2.y);
 }

上記の関数は線分の片側からしか影響を受けませんので、好みに応じて線分の両側から影響を受けるだとか、複数メタボールから影響を受けるだとかに改造します。また、始点のみ拘束するならば回転と拡大縮小はせずとも、平行移動だけで補正が完了します。

円をメタボールで潰す

このページ全体が絶賛開発中であり、だいたいでええやろの精神で構築されていることはもちろんですが、とりわけ以下のやり方は途上もいいとこです。

・円の前に任意ポリラインに対するメタボール変形を試みたので、ややこしいwhileループなんかが入ってたりします。円対メタボールならループを１つに統合できるかと思われます。
・resolutionだのとついてる引数は、直線だの曲線だの、円だのスプラインだのポリラインだのの全体長に対する比です。線分なら0-1、円なら0-2*PI、スプラインだと多分0-(次数-1)とかだったりします。ポリラインは全体を0-1としていたり、ポリライン座標間を0-1としていたり、いろいろです。
・resolutionが異なると、メタボール変形後の座標数が変わったりします。

//近似円新規作成型
List<PVector> CalcuMetaballCircle(
 PVector circle_center, float circle_radius, float circle_resolution, 
 PVector metaball_center, float metaball_radius, float metaball_attenuation, float metaball_resolution)
{
 var circum = MakeCircleOpen(circle_center,circle_radius,circle_resolution);
 return CalcuMetaballCircle(circle_center,circle_radius,circum,metaball_center,metaball_radius,metaball_attenuation,metaball_resolution);
}

List<PVector> CalcuMetaballCircle(
 PVector circle_center, float circle_radius, List<PVector> circle_circumference, 
 PVector metaball_center, float metaball_radius, float metaball_attenuation, float metaball_resolution)
{
 List<PVector> ret = new ArrayList<PVector>();     
 float current_t = 0;  
 int n = circle_circumference.size();
 float unit_radian = (2*PI/(float)n);
 for(int i = 0; i<circle_circumference.size(); i++)
 {    
   int io = (i+1)%n;
   float radian_o = io*unit_radian;      //indexまでのradian(t)  
   var v2_t = map(radian_o,0,2*PI,0,1);       
   //法線に相当
   PVector c2c = circle_center.copy().sub(metaball_center);

   while(current_t<v2_t)
   {          
     var va = GetCircleVertex(circle_center,circle_radius,map(current_t,0,1,0,2*PI));    
     var fx = MetaballCircle_t(va,metaball_center,metaball_radius,metaball_attenuation);
     var lfx = c2c.copy().normalize().mult(fx);
     ret.add(va.copy().add(lfx));      
     current_t=current_t+metaball_resolution;      
   }
 }//for i
 //戻さない方が自然
 //AttachCenterCOGRef(circle_center1, ret);
 return ret;
}

float MetaballCircle_t(
 PVector on_circum_pos,
 PVector metaball_center, float metaball_radius, float metaball_attenuation)
{
 float metaball_circum = 2*PI*metaball_radius;  
 var sx = on_circum_pos.copy().sub(metaball_center).mag()/metaball_circum;  
 var e = metaball_radius*exp(-metaball_attenuation*sx*sx);   
 return e;
}

//最後閉じない
static List<PVector> MakeCircleOpen(PVector circle_center, float radius, float unit_radian)
{
 float start_radian = 0;
 return MakeCircleOpen(circle_center,radius, start_radian, unit_radian);
}   
//最後閉じない
static List<PVector> MakeCircleOpen(PVector circle_center, PVector radius_vector, float unit_radian)
{
 float radius = radius_vector.mag();
 float start_radian = VectorMethod.CalcuAngleRadian360(radius_vector);
 return MakeCircleOpen(circle_center,radius,start_radian, unit_radian);
}   
//最後閉じない
static List<PVector> MakeCircleOpen(PVector circle_center, float radius, float start_radian, float unit_radian)
{
 var ret = new ArrayList<PVector>();
 for(float radian = 0; radian<2*PI; radian+=unit_radian)
 {
   float nx = circle_center.x+radius*cos(start_radian+radian);
   float ny = circle_center.y+radius*sin(start_radian+radian);        
   ret.add(new PVector(nx,ny));
 } 
 return ret;
}  
PVector GetCircleVertex(PVector circle_center, float radius, float radian)
{
 float nx = circle_center.x+radius*cos(radian);
 float ny = circle_center.y+radius*sin(radian);        
 return new PVector(nx,ny);     
}

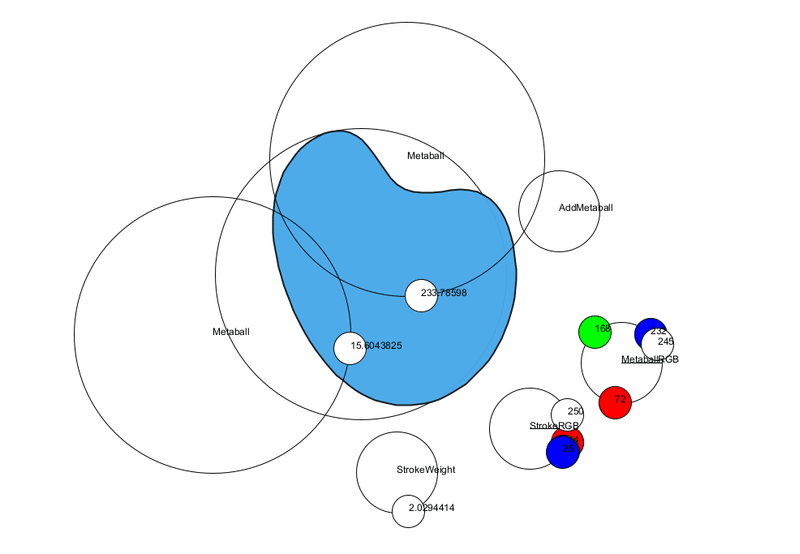
色々と試みた例。

この記事が気に入ったらサポートをしてみませんか？