最上もが日記①#駒場現代物理学2019

講義の（筆者の解釈による）概要と（筆者による勝手な）補足（というか蛇足）です（筆者による補足には※印をつけてあります）．自身の勉強（主に，物理と文章の練習）と備忘のために書きます．

※初期公開時から多少修正しました（匿名性を高めました）．

◆はじめに

学習院大の熱力学の大家T先生が続けられていたT大の教養課程の名物講義「現代物理学」．長い間，出席してみたいと思っていましたが，願いかなわず，今年やっと（初回は）出席することが出来ました．2017年から担当がO先生へ交代となっており，T先生の講義を受けられないのは残念ではありますが，O先生も（Twitterでしか存じ上げないものの）ストイックな科学者の中の科学者という感じの先生ですから，もちろん期待は高まります．

この講座は毎年テーマが異なるのですが，今年は「物理「的」数学」ということでした．単に「物理数学」と言えば，物理で扱う（道具としての）数学という意味になりますが，O先生の意図するところは，「物理的」に数学を扱うということのようです．どういうことかは具体的な講義内容にはいればおぼろ見えてくると思います．

◆端緒としての（数学の）問題

端緒として，次のような問題を考えてみよう．

図1のように正方形の頂点をなす4点A, B, C, Dがあるとき，これらのすべての点が行き来できるような経路のうち，総経路長が最小になるものを求めよ．

図1

各点のつなぎ方として，図2や図3のようなものはすぐに思い浮かぶだろう．簡単のため，線分ABの長さを1とすると，図2の場合の総経路長は3であり，図3の場合は2\sqrt{2}~2.8となって，図2の場合よりは図3の場合の方が短いことが分かる．

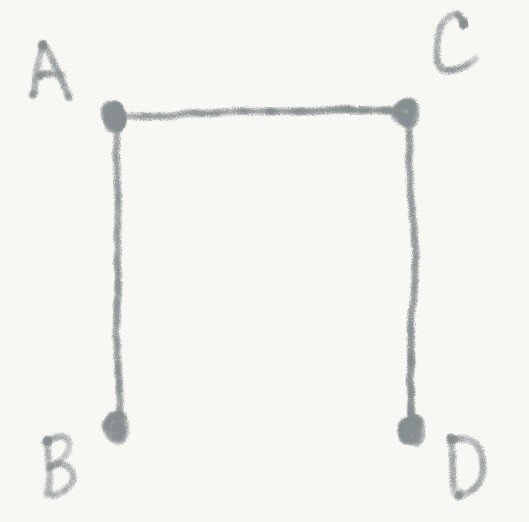
図2

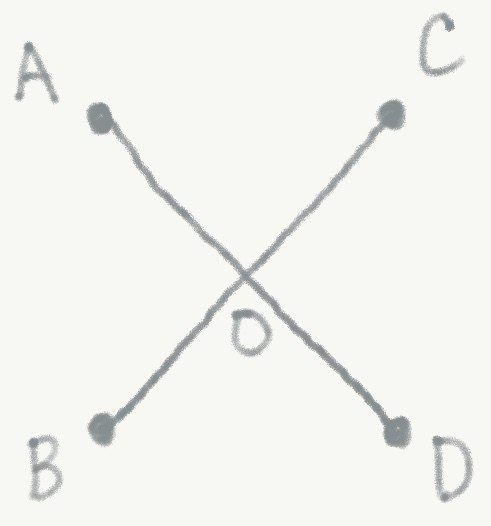
図3

図3の場合を拡張して，図4のような場合を考えると，図3の場合よりもっと総経路長を短くできる．総経路長をL，線分XYの長さをxとし，Lをxの関数と見なす．すると，x=1-\frac{1}{\sqrt{3}}のときに，L(x)が最小となることが（高校程度の）計算ですぐ分かり，このとき，L=1+\sqrt{3}~2.7となる．実はこの場合が他のどの場合よりも総経路長が短いことが分かっている．

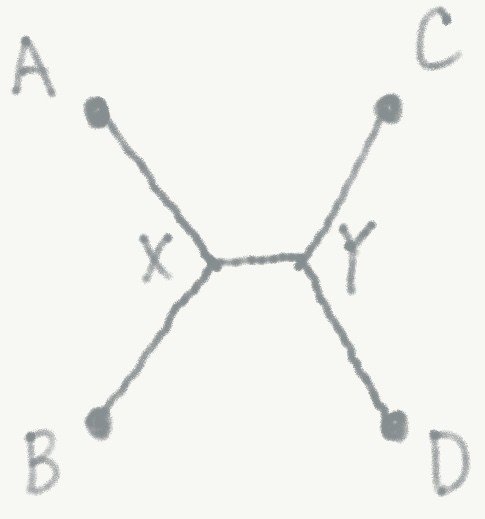
図4

※　この問題に関して検索する際は，「シュタイナー木」というキーワードを用いるとよい．また，この問題そのものの解説は，このページに詳しい．

※　「巡回セールスマン問題」などとも似た問題で，設定自体は，現代の情報科学とも大いに関係してきそうである．

◆展開～数学の問題を物理モデルで表現する

この問題を力学の問題に置き換えてみよう（力学のコトバで言い換えてみよう）．

経路を，張力の大きさが一定の（仮想的な）紐と見なす．張力の大きさをT，全長をLとすれば，この紐が蓄えているエネルギーはU=TLと表されるから，全長Lを最小にする問題は，エネルギーUが最小な状態（すなわち，最も安定な状態）を決定する問題に置き換えることができる．

このように，力学のコトバで表現された問題には，力学的な見方を援用することができる．

一般に，エネルギーが極値をとるとき，力はつりあう．例えば，図2の場合の結節点Oに注目すると，図5を見れば明らかなように，Oに働く力はつりあっている．しかし，このつりあいは不安定である．

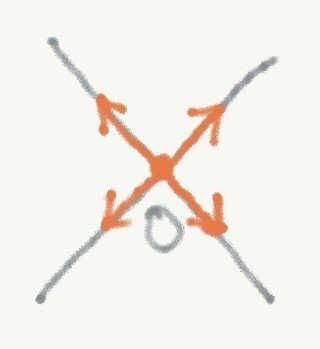
図5

図2の状態から，図3で線分XYが微小な状態にわずかに移行したとする．このとき，結節点Xに働く力は図6のようになって，つりあい得ない．そこでこのような物理状態が仮に実現したとすると，線分XYは伸びていってしまうことになる．

※　少しずらした（摂動を加えた）ときに，系が復元しようとするか否かを調べることは，つりあいの安定性を議論する上での定石である．

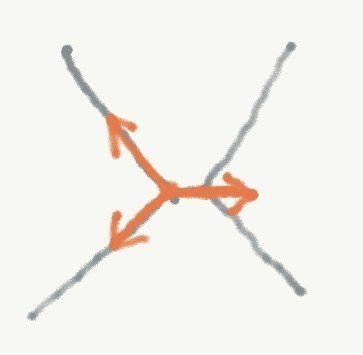
図6

では，どのようなときにつりあうだろうか？結節点Xに働く力が図7のようになればよい（XAとXBとXYがそれぞれ120度の角をなす）．そして，このような場合を作図してみれば，図4でx=1-\frac{1}{\sqrt{3}}とした場合，すなわちLが最小となる場合と見事に一致する．

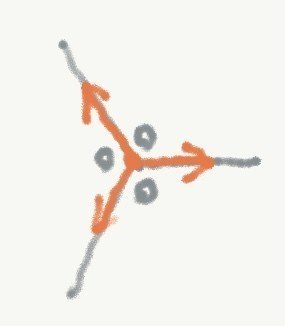
図7

ただし，これが本当にエネルギーが最小の状態かどうかは，保証されず，局所安定解である可能性を否定できないことには注意しておきたい．

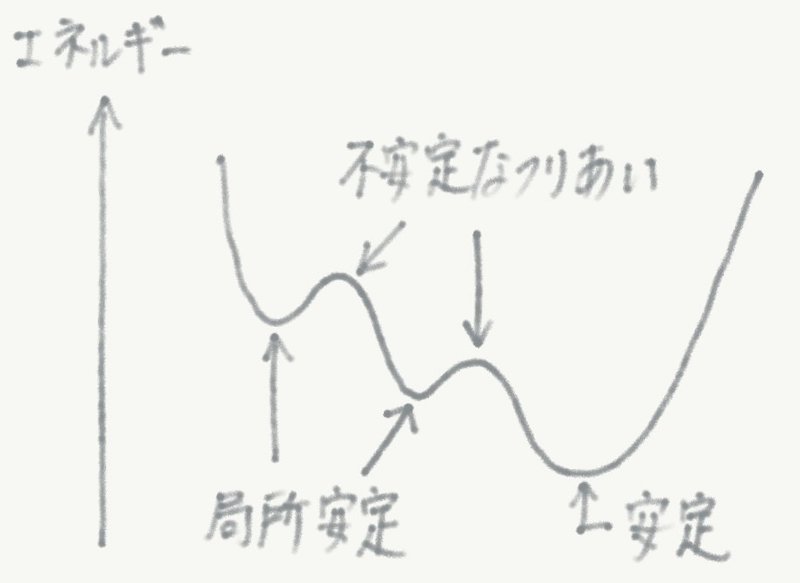
※　物理法則を数学の問題に適用したのではないことに注意．あくまで，数学の問題を物理の問題設定にすり替えただけである（きちんと言えば，数学の問題と等価な物理モデルを作ったのである）．全長Lを最小にすることを，エネルギーUを最小にする問題に言い換えたことにより，力のつりあいの式が利用できるが，力のつり合いの式はエネルギーが極値をとることと数学的に等価であるから，結局は同じことを別の見た目でやっているに過ぎない．とはいえ，数学的な問題に物理的な直感・直観を持ち込めることは，取り扱い上の利点が多々あろう．

※　図2の状態から，図3で線分XYが微小な状態にわずかに移行したときに，力がつりあい得ないことから，XY間がビヨーンと伸びていってしまうイメージを持つと「おぉ！」という気がしないだろうか？しかし，それはL(x)の導関数L'(x)についてL'(0)<0が成り立つという事実の反映にすぎない．くり返すが，数学→物理の言い換えによって，問題の本質が変わるわけではない．

※　以前文系の人が，「経済物理学」について「物理法則を用いて経済現象を扱う」と語っているのを聞いて苦々しく思ったことが忘れられない．もちろん「経済物理学」でやっていることは，複雑すぎる経済現象をより単純な物理モデルで近似的に置き換えて考察することである（と思う）．

※　「物理モデル」を用いることの利点はなんであろうか？イメージが湧きやすいことは，人間が理解を深める（あるいは理解した気になる）助けになる．それだけでなく，人間がイメージすることが出来ると，厳密解は分からなくとも，ヒューリスティックな解を直感的に示せる場合がある．このようなヒューリスティクスが，今後なんらかの本質的な役割を果たす可能性はないだろうか（特にアルゴリズムや認知などの分野で）．

※　今回の話題の次元を1つ上げると「プラトーの問題」を石けん膜を利用して解くことになろう．このページの写真を眺めるととても楽しい．

◆量子アニーリングとの関わりについて

このように，ある種の数学の問題を，物理系で実現される安定な状態を決定する問題に置き換えると，そのような物理系が現実に再現できた場合，その物理系の振る舞いを測定することによって，数学の問題の解を知ることができる．

※　途中のロジックは人間には不明となってしまうが…

具体例として，量子アニーリングを利用した計算機がある．量子アニーリングは，ある種の最適化問題を，無数のスピンを持つ系の安定状態の測定から解く手法である．

※　量子アニーリングについては，このページにあるような解説記事を参照のこと．

◆対称性について

正方形は90度回転の対称性を持つにも関わらず，問題の解は図4のように，対称性が崩れている．このように，物理法則やモデルそのものが持っている対称性が，物理的に実現される安定な状態で破れることを「対称性の自発的な破れ」という．

なお，図4の状態と図4を90度回転した状態はエネルギーの値は同じであるが，そのどちらの状態が実現されるかは，初期条件の微妙な揺らぎで決まる．現在の宇宙の真空の状態は，宇宙初期に起こった自発的対称性の破れにより定まったと考えられている．

※　液体は無秩序で対称性が高いが，温度を下げていって液体が固体になり結晶化すると，非常に秩序だった状態になる．これも（相転移に伴う）対称性の破れのひとつの例である．

◆おわりに

O先生が前日に「そろそろ準備しなければ」とツイートしていたのと裏腹に，流暢な講義でした．また，まだまだ初歩的な内容ではありますが，物性理論の専門家が，背景を知った上で話している余裕と深みを感じることができました．今後も楽しみです．

このような講義が満員となるのはさすがT大と言ったところですが，一方で，200人中女子が10人といない様子は，日本の後進性を如実に表しており，その点は残念としか言いようがありませんでした．